HA-1642-Newton
Isaac
Newton
By
James Gleick

Isaac
Newton
Isaac Newton said
he had seen farther by standing on the shoulders of giants, but he did not
believe it. He was born into a world of darkness, obscurity, and magic; led a
strangely pure and obsessive life, lacking parents, lovers, and friends;
quarreled bitterly with great men who crossed his path; veered at least once to
the brink of madness; cloaked his work in secrecy; and yet discovered more of
the essential core of human knowledge than anyone before or after. He was chief
architect of the modern world. He answered the ancient philosophical riddles of
light and motion, and he effectively discovered gravity. He showed how to
predict the courses of heavenly bodies and so established our place in the
cosmos. He made knowledge a thing of substance: quantitative and exact. He
established principles, and they are called his laws.
Solitude was the
essential part of his genius. As a youth he assimilated or rediscovered most of
the mathematics known to humankind and then invented the calculus‑the
machinery by which the modern world understands change and flow‑but kept
this treasure to himself. He embraced his isolation through his productive
years, devoting himself to the most secret of sciences, alchemy. He feared the
light of exposure, shrank from criticism and controversy, and seldom published
his work at all. Striving to decipher the riddles of the universe, he emulated
the complex secrecy in which he saw them encoded. He stood aloof from other
philosophers even after becoming a national icon – Sir Isaac, Master of the
Mint, President of the Royal Society – his likeness engraved on medals, his
discoveries exalted in verse.
"I don't know
what I may seem to the world," he said before he died, "but, as to
myself, I seem to have been only like a boy playing on the sea‑shore, and
diverting myself in now and then finding a smoother pebble or a prettier shell
than ordinary, whilst the great ocean of truth lay all undiscovered before
me."' An evocative simile, much quoted in the centuries that followed, but
Newton never played at the seashore, boy or man. Born in a remote country
village, the son of an illiterate farmer, he lived in an island nation and
explained how the moon and sun tug at the seas to create tides, but he probably
never set eyes on the ocean. He understood the sea by abstraction and
computation.
His life's path
across the earth's surface covered barely 150 miles: from a hamlet of rural
Lincolnshire southward to the university town of Cambridge and thence to
London. He was born in the bedchamber of a stone farmhouse on Christmas 1642
(as the calendar was reckoned in England‑but the calendar was drifting
out of step with the sun). His father, Isaac Newton, yeoman, had married at
thirty‑five, fallen ill, and died before his son's birth. English had a
word for that: the child was posthumous, thought unlikely to resemble the
father.
This
first Isaac Newton left little trace: some sheep, barley, and simple furniture.
He endorsed his will with his X, for like most of his countrymen he could
neither read nor write. He had worked the land of Woolsthorpe, a place of
woods, open heaths, brooks, and springs, where underneath the thin soil lay a
gray limestone, from which a few dwellings were built to last longer than the
common huts of timber and clay. A road of the Roman Empire passed nearby,
running south and north, a reminder of ancient technology still unsurpassed.
Sometimes children unearthed antique coins or remains of a villa or wall.
The second Isaac
Newton lived to be eighty‑four, gouty and rich. He died in London at the
end of the winter of 1727, a prolonged and excruciating death from a kidney
stone. England for the first time granted a state funeral to a subject whose
attainment lay in the realm of the mind. The Lord Chancellor, two dukes, and
three earls bore the pall, with most of the Royal Society following behind. The
corpse lay in state in Westminster Abbey for eight days and was buried in its
nave. Above the grave was carved an ornate monument in gray and white marble:
the figure of Newton, recumbent; the celestial globe, marked with the path of a
1680 comet; and angelic boys playing with a prism and weighing the sun and
planets. A Latin inscription hailed his "strength of mind almost
divine" and "mathematical principles peculiarly his own" and
declared: "Mortals rejoice that there has existed so great an ornament of
the human race." For England, the continent of Europe, and then the rest
of the world, Newton's story was beginning.
The French writer
calling himself Voltaire had just reached London. He was amazed by the kingly
funeral and exhilarated by all things Newtonian. "A Frenchman arriving in
London finds things very different," he reported. "For us it is the
pressure of the moon that causes the tides of the sea; for the English it is
the sea that gravitates towards the moon, so that when you think that the moon
should give us a high tide, these gentlemen think you should have a low one."
It pleased Voltaire to compare Newton with his nation's late philosophical
hero, Rene Descartes: "For your Cartesians everything is moved by an
impulsion you don't really understand, for Mr Newton it is by gravitation, the
cause of which is hardly better known." The most fundamental conceptions
were new and up for grabs in coffee houses and salons. "In Paris you see
the earth shaped like a melon, in London it is flattened on two sides. For a
Cartesian light exists in the air, for a Newtonian it comes from the sun in six
and a half minutes." Descartes was a dreamer; Newton a sage. Descartes
experienced poetry and love; Newton did not. "In the course of such a long
life he had neither passion nor weakness; he never went near any woman. I have
had that confirmed by the doctor and the surgeon who were with him when he
died."
What Newton learned
remains the essence of what we know, as if by our own intuition. Newton's laws
are our laws. We are Newtonians, fervent and devout, when we speak of forces
and masses, of action and reaction; when we say that a sports team or political
candidate has momentum; when we note the inertia of a tradition or bureaucracy;
and when we stretch out an arm and feel the force of gravity all around,
pulling earthward. Pre‑Newtonians did not feel such a force. Before
Newton the English word gravity denoted
a mood‑‑seriousness, solemnity‑or an intrinsic quality.
Objects could have heaviness or lightness, and the heavy ones tended downward,
where they belonged.
We have assimilated
Newtonianism as knowledge and as faith. We believe our scientists when they
compute the past and future tracks of comets and spaceships. What is more, we
know they do this not by magic but by mere technique. "The landscape has
been so totally changed, the ways of thinking have been so deeply affected,
that it is very hard to get hold of what it was like before,' said the
cosmologist and relativist Hermann Bondi. "It is very hard to realize how
total a change in outlook he produced."
Creation, Newton saw, unfolds from simple rules, patterns iterated over
unlimited distances. So we seek mathematical laws for economic cycles and human
behavior. We deem the universe solvable.
He began with foundation stones of knowledge:
time, space, motion. I do not define
time, space, place, and motion, as being well known to all, he wrote in
midlife ‑ then a reclusive professor, recondite theologian and alchemist,
seldom leaving his room in Trinity College, Cambridge. But he did mean to
define these terms. He salvaged them from the haze of everyday language. He
standardized them. In defining them, he married them, each to the others.
He
dipped his quill in an ink of oak galls and wrote a minuscule Latin script,
crowding the words edge to edge: The
common people conceive those quantities under no other notions but from the
relation they bear to sensible objects. And thence arise certain prejudices....
By then he had written more than a million words and published almost none.
He wrote for himself, careless of food and sleep. He wrote to calculate, laying
down numbers in spidery lines and broad columns. He computed as most people
daydream. The flow of his thought slipped back and forth between English and
Latin. He wrote to read, copying out books and manuscripts verbatim, sometimes
the same text again and again. More determined than joyful, he wrote to reason,
to meditate, and to occupy his febrile mind.
His name betokens a
system of the world. But for Newton himself there was no completeness, only a
questing dynamic, protean, and unfinished. He never fully detached matter and
space from God. He never purged occult, hidden, mystical qualities from his
vision of nature. He sought order and believed in order but never averted his
eyes from the chaos. He of all people was no Newtonian.
Information flowed
faintly and perish ably then, through the still small human species, but he
created a method and a language that triumphed in his lifetime and gained
ascendancy with each passing century. He pushed open a door that led to a new
universe: set in absolute time and space, at once measureless and measurable,
furnished with science and machines, ruled by industry and natural law.
Geometry and motion, motion and geometry: Newton joined them as one. With the
coming of Einstein's relativity, Newtonian science was often said to have been
"overthrown" or "replaced," but that was not so. It had
been buttressed and extended.
"Fortunate
Newton, happy childhood of science!" said Einstein. "Nature to him
was an open book. He stands before us strong, certain, and alone."
Yet he speaks to us
reluctantly and covertly.
Chapter
1 What Imployment Is He Fit For?
Medieval,
in some disrepair, the Woolsthorpe farmhouse nestled into a hill near the River
Witham. With its short front door and shuttered windows, its working kitchen,
and its bare floors of ash and linden laid on reeds, it had belonged to
Newton's forebears for just twenty years. In back stood apple trees. Sheep
grazed for acres around.
Isaac was born in a
small room at the top of the stairs. By the terms of feudal law this house was
a manor and the fatherless boy was its lord, with seigniorial authority over a
handful of tenant farmers in nearby cottages. He could not trace his ancestry
back past his grandfather, Robert, who lay buried in the churchyard nearly a
mile to the east. Still, the boy expected to live managing the farm in the
place of the father he had never known. His mother, Hannah Ayscough, had come
from gentlefolk. Her brother, the Reverend William Ayscough, studied at
Cambridge University on his way to joining the Anglican clergy; now he occupied
a village rectory two miles away. When Isaac was three years old and his
widowed mother near thirty, she accepted a marriage offer from another nearby
rector, Barnabas Smith, a wealthy man twice her age. Smith wanted a wife, not a
stepson; under the negotiated terms of their marriage Hannah abandoned Isaac in
the Woolsthorpe house, leaving him to his grandmother's care.
War flared in the countryside
all through his youth. The decade‑long Great Rebellion began in the year
of his birth: Parliamentarians fighting Royalists, Puritans recoiling from the
idolatry they saw in the Church of England. Motley, mercenary armies skirmished
throughout the Midlands. Pikemen and musketeers sometimes passed through the
fields near Woolsthorpe. Bands of men
plundered farms for supplies. England was at war with itself and also,
increasingly, aware of itself‑its nationhood, its specialness. Divided as
it was, convulsed over ecclesiastical forms and beliefs, the nation carried out
a true revolution. The triumphant Puritans rejected absolutism and denied the
divine right of the monarchy. In 1649, soon after Isaac turned six, Charles
Stuart, the king, was beheaded at the wall of his palace.
This rustic country
covered a thousandth of the world's landmass, cut off from the main continent
since the warming of the planet and the melting of polar ice 13,000 years
before. Plundering, waterborne tribes had settled on its coasts in waves and
diffused into its downs and valleys, where they aggregated in villages. What
they knew or believed about nature depended in part on the uses of technology.
They had learned to employ the power of water and wind to crush, grind, and polish.
The furnace, the forge, and the mill had taken their place in an economy that
thereby grew more specialized and hierarchical. People in England, as in many
human communities, made metal-kettles of copper and brass, rods and nails of
iron. They made glass. These crafts and materials were prerequisites now to a
great leap in knowledge. Other prerequisites were lenses, paper and ink,
mechanical clocks, numeric systems capable of denoting indefinitely small
fractions, and postal services spanning hundreds of miles.
By the time of
Newton's birth, one great city had formed, with about 400,000 people; no other
town was even a tenth as large. England was still a country of villages and
farms, its seasons ordered by the Christian calendar and the rhythms of agriculture:
lambing and calving, haymaking and harvest. Years of harvest failure brought
widespread starvation. Roving laborers and vagrants made up much of the
population. But a class of artisans and merchants was coming into its own:
traders, shopkeepers, apothecaries, glaziers, carpenters, and surveyors, all
developing a practical, mechanical view of knowledge. They used numbers and made tools. The nucleus of a manufacturing
economy was taking shape.
When Isaac was old
enough, he walked to the village dame school, where he learned to read and
studied the Bible and chanted arithmetic tables. He was small for his age,
lonely and abandoned. Sometimes he wished his step-father dead, and his mother,
too: in a rage he threatened to burn their house down over them. Sometimes he
wished himself dead and knew the wish for a sin.
On bright days
sunlight crept along the wall. Darkness as well as light seemed to fall from
the window ‑ or was it from the eye? No one knew. The sun projected slant
edges, a dynamic echo of the window frame in light and shadow, sometimes sharp
and sometimes blurred, expressing a three‑dimensional geometry of
intersecting planes. The particulars were hard to visualize, though the sun was
the most regular of heavenly objects, the one whose cycles already defined the
measures of time. Isaac scratched crude geometric figures, circles with arcs
inscribed, and hammered wooden pegs into the walls and the ground to measure
time exactly, to the nearest quarter‑hour. He cut sun‑dials into stone and charted the shadows cast by
their gnomons. This meant seeing time as akin to space, duration as length, the
length of an arc. He measured small distances with strings and made a
translation between inches and minutes of an hour. He had to revise this
translation methodically as the seasons changed. Across the day the sun rose
and fell; across the year its position in the sky shifted slightly against the
fixed stars and traced a slowly twisting figure eight, a figure invisible
except to the mind's eye. Isaac grew conscious of this pattern long before he
understood it as the product of two oddities, the earth's elliptical orbit and
a tilt in its axis.
At Woolsthorpe
anyone who cared to know the hour consulted Isaac's dials. "0 God!
Methinks it were a happy life," said Shakespeare's Henry VI, "to
carve out dials quaintly, point by point, thereby to see the minutes how they
run." Sun‑dials‑shadow‑clocks‑still told most
people the time, though at some churches the hour could be read from mechanical
clocks. At night the stars turned in the blue vault of the sky; the moon waxed
and waned and traced its own path, much like the sun's, yet not exactly these
great globes, ruling the seasons, lighting the day and night, connected as if
by invisible cords. Sun‑dials embodied practical knowledge that had been
refined over millennia. With cruder sun‑dials, the hours were unequal and
varied with the seasons. Better versions achieved precision and encouraged an
altered sense of time itself: not just as a recurring cycle, or a mystical
quality influencing events, but as duration, measurable, a dimension. Still, no
one could perfect or even understand sun‑dials until all the shifting
pieces of a puzzle had been assembled: the shadows, the rhythms, the orbits of
planets, the special geometry of the ellipse, the attraction of matter by
matter. It was all one problem.
When Isaac was ten,
in 1653, Barnabas Smith died, and Hannah returned to Woolsthorpe, bringing
three new children with her. She sent Isaac off to school, eight miles up the Great
North Road, to Grantham, a market town of a few hundred families ‑ now a
garrison town, too. Grantham had two inns, a church, a guild hall, an
apothecary, and two mills for grinding corn and malt." Eight miles was too
far to walk each day; Isaac boarded with the apothecary, William Clarke, on
High Street. The boy slept in the garret and left signs of his presence,
carving his name into the boards and drawing in charcoal on the walls: birds
and beasts, men and ships, and pure abstract circles and triangles.
At the Kings
School, one room, with strict Puritan discipline, Henry Stokes, schoolmaster,
taught eighty boys Latin, theology, and some Greek and Hebrew. In most English
schools that would have been all, but Stokes added some practical arithmetic for
his prospective farmers: mostly about measurement of areas and shapes,
algorithms for surveying, marking fields by the chain, calculating acres
(though the acre still varied from one county to the next, or according to the
land's richness). He offered a bit more
than a farmer would need: how to inscribe regular polygons in a circle and
compute the length of each side, as Archimedes had done to estimate pi. Isaac
scratched Archimedes' diagrams in the wall. He entered the lowest form at the
age of twelve, lonely, anxious, and competitive. He fought with other boys in
the churchyard; sometimes noses were bloodied. He filled a Latin exercise book
with unselfconscious phrases, some copied, others invented, a grim stream of
thought: A little fellow; My poore help;
Hee is paile; There is no room for me to sit; In the top of the house‑In
the bottom of hell; What imployment is he fit for? What is hee good for? He
despaired. I will make an end. I cannot
but weepe. I know not what to doe.
Barely
sixty lifetimes had passed since people began to record knowledge as symbols on
stone or parchment. England's first paper mill opened at the end of the
sixteenth century, on the Deptford River. Paper was prized, and the written
word played a small part in daily life. Most of what people thought remained
unrecorded; most of what they recorded was hidden or lost. Yet to some it
seemed a time of information surfeit. "I hear new news every day,"
wrote the vicar Robert Burton, attuned as he was‑virtually living in the
Bodleian Library at Oxford‑to the transmission and storage of data:
those ordinary
rumours of war, plagues, fires, inundations, thefts, murders, massacres,
meteors, comets, spectrums, prodigies, apparitions, . . . and such like, which
these tempestuous times afford. . . . New books every day, pamphlets,
currantoes, stories, whole catalogues of volumes of all sorts, new paradoxes,
opinions, schisms, heresies, controversies in philosophy, religion &c
Burton was
attempting to assemble all previous knowledge into a single rambling,
discursive, encyclopedic book of his own. He made no apology for his resolute
plagiarism; or, rather, he apologized this way: "A dwarf standing on the
shoulders of a Giant may see farther than a Giant himself." 16 He tried
to make sense of rare volumes from abroad, which proposed fantastic and
contradictory schemes of the universe ‑ from Tycho, Galileo, Kepler, and
Copernicus. He tried to reconcile them with ancient wisdom.
Did the earth move? Copernicus had revived that notion, Ccnot as a
truth, but a supposition." Several others agreed. "For if the Earth
be the Center of the World, stand still, as most received opinion is," and
the celestial spheres revolve around it, then the heavens must move with
implausible speed. This followed from measurements of the distance of sun and
stars. Burton borrowed (and mangled) some arithmetic. "A man could not
ride so much ground, going 40 miles a day, in 2,904 years, as the Firmament
goes in 24 hours; or so much in 203 years, as the said Firmament in one minute;
which seems incredible." People were looking at the stars through spy‑glasses;
Burton himself had seen Jupiter through a glass eight feet long and agreed with
Galileo that this wanderer had its own moons.
He was forced to consider issues of shifting viewpoint, though there
was no ready language for expressing such conundrums: "If a man's eye were
in the Firmament, he should not at all discern that great annual motion of the
earth, but it would still appear an indivisible point." If a man's eye
could be so far away, why not a man? Imaginations ran free. "If the earth
move, it is a Planet, & shines to them in the Moon, & to the other
Planetary Inhabitants, as the Moon and they to us upon the earth."
We may likewise insert ... there be infinite Worlds, and infinite
earths or systems, in infinite aether, . . . and so, by consequence, there are
infinite habitable worlds: what hinders? ... It is a difficult knot to untie.
Especially difficult because so many different authorities threw forth
so many hypotheses: our modern divines, those heathen philosophers, heretics,
schismatics, the Church of Rome. "Our latter Mathematicians have rolled
all the stones that may be stirred: and ... fabricated new systems of the
World, out of their own Daedalean heads."
Many races of men have studied the face of the sky throughout history,
Burton said, and now the day was coming when God would reveal its hidden
mysteries. Tempestuous times, indeed.
But new books every day did not find their
way to rural Lincolnshire. Newton's stepfather, Smith, had owned books, on
Christian subjects. The apothecary Clarke also owned books. Smith even
possessed blank paper, in a large commonplace book that he had kept for forty
years. He painstakingly numbered the pages, inscribed theological headings atop
the first few, and otherwise left it almost entirely empty. Some time after his
death this trove of paper came into Isaac's possession. Before that, in
Grantham, with two and a half pence his mother had given him, Isaac was able to
buy a tiny notebook, sewn sheets bound in vellum. He asserted his ownership
with an inscription: Isacus Newton hunc
librum possidet. Over many months
he filled the pages with meticulous script, the letters and numerals often less
than one‑sixteenth of an inch high. He began at both ends and worked
toward the middle. Mainly he copied a book of secrets and magic printed in
London several years earlier: John Bate's Mysteryes
of Nature andArt, a scrap book, rambling and yet encyclopedic in its
intent.
He copied instructions
on drawing. "Let the thing which intend to draw stand before you, so the
light be not hindered from falling upon it ... .. If you express the sunn make
it riseing or setting behind some hill; but never express the moon or starrs
but up on necessity." He copied recipes for making colors and inks and
salves and powders and waters. "A sea colour. Take privet berries when the
sun entreth into Libra, about the 13th of September, dry them in the sunn; then
bruise them & steep them." Colors fascinated him. He catalogued
several dozen, finely and pragmatically distinguished: purple, crimson, green,
another green, a light green, russet, a brown blue, "colours for naked
pictures," cc colours for dead corpes," charcoal black and seacoal
black. He copied techniques for melting metal (in a shell), catching‑
birds ("set black wine for them to drink where they come " ),
engraving on a flint, making pearls of chalk.
Living with Clarke,
apothecary and chemist, he learned to grind with mortar and pestle; he
practiced roasting and boiling and mixing; he formed chemicals into pellets, to
be dried in the sun. He wrote down cures, remedies, and admonitions:
THINGS
HURTFULL FOR THE EYES
Garlick Onions & Leeks .... Gooing too
suddaine after meals. Hot wines. Cold ayre .... Much blood‑letting ...
dust. ffire. much weeping....
Bate's
book mixed Aristotelianism and folklore: "sundry Experiments both
serviceable and delightfull, which because they are confusedly intermixed, I
have entituled them Extravagants." Isaac
copied that word atop several pages. Bate described and illustrated many forms
of waterworks and fireworks, and Isaac spent hours cutting wood with his knife,
building ingenious watermills and windmills. Grantham town was building a new
mill; Isaac followed its progress and made a model, internalizing the whirring
and pounding of the machine and the principles that govern gears, levers,
rollers and pulley wheels. In his garret he constructed a water‑clock,
four feet high, from a wooden box, with an hour hand on a painted dial. He made
paper lanterns. He crafted kites and sent them aloft at night trailing lanterns
ablaze‑lights in the black sky to frighten the neighbors.
Bate offered
knowledge as play, but with a nod to system: "the four elements, Fier,
Ayer, Water, and Earth, and the prima
Principia," he wrote. This venerable four‑part scheme‑with
its corollary powers: dry, cool, warm, and moist‑‑expressed a
desire to organize, classify and name the world's elements, in the absence of
mathematical and technological tools. Simple wisdom covered motion, too. Bate
explained: "Their light parts ascend upwards; and those that are more
grosse & heavy, do the contrary.
Isaac omitted these
principles from his copying. He crowded his tiny pages with astronomical tables
related to sun‑dialing, followed by an elaborate computation of the
calendar for the next twenty‑eight years. He copied lists of words,
adding as many of his own as came to mind. Across forty‑two notebook
pages he organized 2,400 nouns in columns under subject headings:
Artes,
Trades, & Sciences: ... Apothecary ... Armourer
Astrologer
Astronomer ... Diseases: ... Gobbertooth ...
Gout
... Gangreene ... Gunshott... Kindred, & Titles:
Bridegroome
... Brother Bastard Barron ... Brawler Babler
...
Brownist Benjamite ... Father Fornicator...
Thoughts of family were no balm to this troubled soul. Nevertheless, in
the fall of 1659, when Isaac was sixteen years old, his mother summoned him
home to be a farmer.
Chapter
2 Some Philosophical Questions
He
did not know what he wanted to be or do, but it was not tend sheep or follow
the plow and the dung cart. He spent more time gathering herbs and lying with a
book among the asphodel and moonwort, out of the household's sight.' He built
waterwheels in the stream while his sheep trampled the neighbors' barley. He
watched the flow of water, over wood and around rocks, noting the whorls and
eddies and waves, gaining a sense of fluid motion.2 He defied his mother and
scolded his half‑sisters. He was
fined in the manor court for allowing his swine to trespass and his fences to
lie in disrepair.
His Grantham
schoolmaster, Stokes, and his mother's brother, the rector William Ayscough,
finally intervened. Ayscough had prepared for the clergy at the College of the
Holy and Undivided Trinity, the greatest of the sixteen colleges at the
University of Cambridge, so they arranged for Isaac to be sent there. He made
the journey south, three days and two nights, and was admitted in June 1661.
Cambridge recognized students in three categories: noblemen, who dined at high
table, wore sophisticated gowns, and received degrees with little examination;
pensioners, who paid for tuition and board and aimed, mainly, for the Anglican
ministry; and sizars, who earned their keep by menial service to other students,
running errands, waiting on them at meals, and eating their leftovers. The
widowed Hannah Smith was wealthy now, by the standards of the countryside, but
chose to provide her son little money; he entered Trinity College as a
subsizar. He had enough for his immediate needs: a chamber pot; a notebook of
140 blank pages, three and a half by five and a half inches, with leather
covers; "a quart bottle and ink to fill it"; candles for many long
nights, and a lock for his desk. For a
tutor he was assigned an indifferent scholar of Greek. Otherwise he kept to
himself.
He felt learning as
a form of obsession, a worthy pursuit, in God's service, but potentially
prideful as well. He taught himself a shorthand of esoteric symbols‑this
served both to save paper and encrypt his writing‑and he used it, at a
moment of spiritual crisis, to record a catalogue of his sins. Among them were neglecting to pray, negligence at the
chapel, and variations on the theme of falling short in piety and devotion.
He rebuked himself for a dozen ways of breaching the Sabbath. On one Sunday he
had whittled a quill pen and then lied about it. He confessed uncleane thoughts words and actions and
dreamese. He regretted, or tried to regret, setting my heart on money learning pleasure more than Thee. Money, learning, pleasure: three sirens
calling his heart. Of these, neither money nor pleasure came in abundance.
The Civil War had
ended and so had the Protectorate of Oliver Cromwell, dead from malaria, buried
and then exhumed so his head could be stuck on a pole atop Westminster Hall.
During the rebellion Puritan reformers had gained control of Cambridge and
purged the colleges of many Royalist scholars. Now, with the restoration of
Charles II to the crown, Puritans were purged, Cromwell was hanged in effigy,
and the university's records from the Protectorate years were burned. This
riverside town was a place of ferment, fifty miles from London, a hundredth its
size, a crossroads for information and commerce. Each year between harvest and
plowing, tradesmen gathered for Stourbridge Fair, England's largest: a giant
market for wool and hops, metal‑ware and glass‑ware, silk and
stationery, books, toys, and musical instruments‑a bedlam of languages
and apparel, and "an Abstract of all sorts of mankind," as a
pamphleteer described it. Newton, scrupulous with his limited funds, bought
books there and, one year, a glass prism ‑ a toy, imprecisely ground,
flawed with air bubbles. Often enough, the complex human traffic had another
consequence: Cambridge suffered visitations of plague.
The curriculum had
grown stagnant. It followed the scholastic tradition laid down in the
university's medieval beginnings: the study of texts from disintegrated
Mediterranean cultures, preserved in Christian and Islamic sanctuaries through
a thousand years of European upheaval. The single authority in all the realms
of secular knowledge was Aristotle ‑‑ doctor's son, student of
Plato, and collector of books. Logic, ethics, and rhetoric were all his, and so
‑ to the extent they were studied at all ‑ were cosmology and
mechanics. The Aristotelian canon enshrined systematization and rigor,
categories and rules. It formed an edifice of reason: knowledge about
knowledge. Supplemented by ancient poets and medieval divines, it was a
complete education, which scarcely changed from generation to generation.
Newton began by reading closely, but not finishing, the Organon and the Nicomachean
Ethics ("For the things we have to learn before we can do them, we
learn by doing them") .
He read Aristotle
through a mist of changing languages, along with a body of commentary and
disputation. The words crossed and overlapped. Aristotle's was a world of
substances. A substance possesses qualities and properties, which taken
together amount to a form, depending
ultimately on its essence. Properties can change; we call this motion. Motion is action, change, and
life. It is an indispensable partner of time;
the one could not exist without the other. If we understood the cause of
motion, we would understand the cause of the world.
For Aristotle
motion included pushing, pulling, carrying, and twirling; combining and
separating; waxing and waning. Things in motion included a peach ripening, a fish
swimming, water warming over a fire, a child growing into an adult, an apple
falling from a tree. The heavy thing
and the light thing move to their proper positions: the light thing up and the
heavy thing down. Some motion is
natural; some violent and unnatural. Both kinds revealed the connections
between things. "Everything that is in motion must be moved by
something," Aristotle asserted (and proved, by knotted logic). A thing cannot be at once mover and moved. This simple truth implied a first mover, put in motion by no
other, to break what must otherwise be an infinite loop:
Since everything that is in motion must be moved by something, let us
take the case in which a thing is in locomotion and is moved by something that
is itself in motion, and that by something else, and so on continually: then
the series cannot go on to infinity, but there must be some first mover.
To the Christian fathers, this first
mover could only be God. It was a testament to how far pure reason could take a
philosopher; and to how involuted and self‑referential a chain of
reasoning could become, with nothing to feed on but itself.
This all‑embracing
sense of motion left little place for quantity, measurement, and number. If
objects in motion could include a piece of bronze becoming a statue, then
philosophers were not ready to make fine distinctions, like the distinction
between velocity and acceleration. Indeed, the Greeks had a principled
resistance to mathematicizing our corruptible, flawed, sublunary world. Geometry
belonged to the celestial sphere; it might relate music and the stars, but
projectiles of rock or metal were inappropriate objects for mathematical
treatment. So technology, advancing, exposed Aristotelian mechanics as quaint
and impotent. Gunners understood that a cannonball, once in flight, was no
longer moved by anything but a ghostly memory of the explosion inside the iron
barrel; and they were learning, roughly, to compute the trajectories of their
projectiles. Pendulums, in clockwork, however crude, demanded a mathematical
view of motion. And in turn the clockwork made measurement possible‑first
hours, then minutes. Of an object falling from a tower or rolling down an
inclined plane, people could begin to ask: what is the distance? what is the
time?
What, therefore, is the velocity? And how
does the velocity, itself, change?
Nor
was Aristotle's cosmology faring well outside Cambridge's gates. It was
harmonious and immutable: crystalline spheres round the earth, solid and
invisible, carrying the celestial orbs within them. Ptolemy had perfected his
universe and then, for hundreds of years, Christian astronomers embraced and
extended it, reconciled it with biblical scripture, and added a heaven of
heavens, deep and pure, perhaps infinite, the home of God and angels, beyond
the sphere of fixed stars. But as stargazers made increasingly detailed
notations, they catalogued planetary motions too irregular for concentric
spheres. They saw freaks and impurities, such as comets glowing and vanishing.
By the 1660s ‑ new news every day
‑ readers of esoterica knew well enough that the earth was a planet and
that the planets orbited the sun. Newton's notes began to include measurements
of the apparent magnitude of stars.
Although the
library of Trinity College had more than three thousand books, students could
enter only in the company of a fellow. Still, Newton found his way to new ideas
and polemics: from the French philosopher Rene Descartes, and the Italian
astronomer Galileo Galilei, who had died in the year of Newton's birth.
Descartes proposed a geometrical and mechanical philosophy. He imagined a
universe filled throughout with invisible substance, forming great vortices
that sweep the planets and stars forward. Galileo, meanwhile, applied
geometrical thinking to the problem of motion. Both men defied Aristotle
explicitly Galileo by claiming that all bodies are made of the same stuff,
which is heavy, and therefore fall at the same rate.
Not the same speed, however. After long gestation,
Galileo created a concept of uniform acceleration. He considered motion as a
state rather than a process. Without ever using a word such as inertia, he nonetheless conceived that
bodies have a tendency to remain in motion or to remain motionless. The next
step demanded experiment and measure. He measured time with a water‑clock.
He rolled balls down ramps and concluded, wrongly, that their speed varied in
proportion to the distance they rolled. Later, trying to understand free fall,
he reached the modern definition, correctly assimilating units of distance,
units of speed, and units of time. Newton began to absorb this, at second or
third hand; Galileo had written mostly in Italian, a language few in England
could read.
In
Newton's second year, having filled the beginning and end of his notebook with
Aristotle, he started a new section deep inside: Questiones quadam philosophic&‑some philosophical
questions. He set authority aside. Later he came back to this page and
inscribed an epigraph borrowed from Aristotle's justification for dissenting
from his teacher. Aristotle had said, "Plato is my friend, but truth my
greater friend." Newton inserted Aristotle's name in sequence: Amicus Plato amicus Aristoteles magis amica
veritas. He made a new beginning.
He set down his knowledge of the world, organized under elemental headings,
expressed as questions, based sometimes on his reading, sometimes on
speculation. It showed how little was known, altogether. Tlie choice of topics ‑
forty‑five in all ‑ suggested a foundation for a new natural philosophy.
Of
the First Matter. Of Atoms. Could he know, by
the force of logic, whether matter was continuous and infinitely divisible, or
discontinuous and discrete? Were its ultimate parts mathematical points or
actual atoms? Since a mathematical point lacks body or dimension ‑
"is but an imaginary entity" ‑ it seemed implausible that even
an infinite number of them could combine to form matter with real
extension, even if bits of vacuum
("interspersed inanities") separated the parts. The question of God's
role, as creator, could be dangerous territory. "Tis a contradiction to
say the first matter depends on some other subject" ‑ in parentheses
he added, "except God"; then, on second thought, he crossed that out ‑
"since that implies some former matter on which it must depend."
Reasoning led him, as it had led ancient Greeks, to atoms‑not by
observation or experiment, but by eliminating alternatives. Newton declared
himself a corpuscularian and an atomist. "'Me first matter must be attoms.
And that Matter may be so small as to be indiscernible." Very small, but
finite, not zero. Indiscernible, but unbreakable and indivisible. This was an
unsettled conception, because Newton also saw a world of smooth change, of
curves, and of flow. What about the smallest parts of time and motion? Were
these continuous or discrete?
Quantity.
Place. "Extension is related to places, as time
to days yeares &c.” He invoked God
on another controversial question: Is space finite or infinite? Not the
imaginary abstract space of geometers, but the real space in which we live.
Infinite, surely! "To say that extension is but indefinite" ‑
Descartes said this, in fact ‑ "is as much to say God is but
indefinitely perfect because wee cannot apprehend his whole perfection."
Time
and Eternity. No abstract disputation here; he just
sketched a wheel‑shaped clock, to be driven by water or sand, and raised
wholly practical questions about making clocks with various materials, such as
"metalline globular dust." Only then did he reach Motion, and again, he began by looking
for the root constituents, the equivalent of atoms. Motion led to Celestiall
Matter & Orbes‑which took Newton, encountering the early echoes
of Continental thought, to Descartes. In Descartes's universe, there could be
no vacuum, for the universe was space, and space meant extension, and extension
surely implied substance. Also, the world's principles were mechanical: all
action propagated through contact, one object directly pushing another, no
mystical influences from afar.
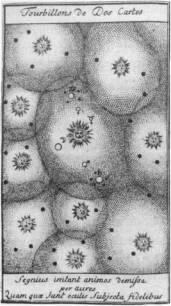
In the cosmos of Descartes, matter fills all space and
forms whirling vortices.
So
a vacuum could not transmit light. Light was a form of pression, Descartes said‑imaginatively,
because philosophers had barely begun to conceive of pressure as a quality that
an invisible fluid, the air, could possess. But now Newton had heard of Robert
Boyle's experiments with an air-pump, and pressure was the word Boyle used in
this new sense. Newton began again:
Whether Cartes his first element can turne about the vortex & yet
drive the matter of it continually from the (**D**) [sun] to produce light, & spend most of its motion in filling
up the chinks between the globuli.
From matter to motion, to light, and to the structure of the cosmos.
The sun drove the vortex by its beams. The ubiquitous vortex could drive
anything: Newton sketched some ideas for perpetual motion machines. But light
itself played a delicate part in the Cartesian scheme, and Newton, attempting
to take Descartes literally, already sensed contradictions. Pressure does not
restrict itself to straight lines; vortices whirl around corners. "Light
cannot be by pression," Newton asserted, "for then wee should see in
the night a [s] wel or better than in the day we should se[e] a bright light
above us becaus we are pressed downewards. . . . " Eclipses should never
darken the sky. "A man goeing or running would see in the night. When a
fire or candle is extinguished we lookeing another way should see a
light."
Another elusive
word, gravity, began to appear in the Questiones.
Its meanings darted here and there. It served as half of a linked pair:
Gravity & Levity. It represented the tendency of a body to descend, ever
downward . But how could this happen? "The matter causing gravity must
pass through all the pores of a body. It must ascend againe, for else the
bowells of the earth must have had large cavitys & inanitys to containe it
in. . . . " It must be crowded in that unimaginable
place, the center of the earth ‑ all the world's streams coming home.
"When the streames meet on all sides in the midst of the Earth they must
needs be coarcted into a narrow roome & closely press together."

Then again, perhaps an object's gravity was inherent, a quantity to be
exactly measured, even if it varied from place to place: "The aravity of a
body in diverse places as at the top and bottom 0 a hill, in different
latitudes &c. may be measured by an instrument" ‑ he sketched a
balance scale. He speculated about
"rays of gravity." Then, gravity could also refer to a body's
tendency to move, not downward, but in any direction; its tendency to remain in
motion, once started. If such a tendency existed, no language yet had a word
for it. Newton considered the problem
of the cannonball, still rising, long after leaving the gun. "Violent
motion is made" he struck the word made ‑ "continued either by
the aire or by motion" ‑ struck the word motion and replaced it with
force:
Violent motion is made
continued either by the aire or by motion force imprest or by the
natural gravity in the body moved.
Yet how could the cannonball be
helped along by the air? He noted that the air crowds more upon the front of a
projectile than on the rear., "& must therefore rather hinder
it." So the continuing motion must come from some natural tendency in the
object. But‑gravioP
Some of his topics‑for example,
Fluidity Stability Humidity Siccity20‑never progressed past a heading.
No matter. He had set out his questions. Of Heate
& Cold. Atraction Magneticall.
Colours. Sounds. Generation & Coruption. Memory. They formed a program, girded with measurements, clocks and
scales, experiments both practical and imaginary. Its ambition encompassed the
whole of nature.
One
more mystery: the Flux & Reflux of the Sea. He considered a way to test
whether the moon's "pressing the atmosphere" causes the tides. Fill a
tube with mercury or water; seal the top; "the liquor will sink three or
four inches below it leaving a vacuum (perhaps)"; then as the air is
pressed by the moon, see if the water will rise or fall. He wondered whether
the sea level rose by day and fell by night; whether it was higher in the
morning or evening. Though fishermen and sailors around the globe had studied
the tides for thousands of years, people had not amassed enough data to settle
those questions.
Chapter
3 To Resolve Problems by Motion
Cambridge
in 1664 had for the first time in its history a professor of mathematics, Isaac
Barrow, another former Trinity College sizar, a decade older than Newton.
Barrow had first studied Greek and theology; then left Cambridge, learned
medicine, more theology, church history, and astronomy, and finally turned to
geometry. Newton attended Barrow's first lectures. He was standing for
examinations that year, on his way to being elected a scholar, and it was
Barrow who examined him, mainly on the Elements
of Euclid. He had not studied it before. At Stourbridge Fair he found a
book of astrology and was brought up short by a diagram that required an
understanding of trigonometry ‑
more than any Cambridge student was meant to know. He bought and borrowed more
books. Before long, in a few texts, he had at hand a precis of the advanced
mathematics available on the continent of Europe. He bought Franz van
Schooten's Miscellanies and his Latin
translation of Descartes's difficult masterpiece, La Geometrie; then William Oughtred's Clavis Mathematica and John Wallis's Arithmetica Infinitorum. This reading remained far from
comprehensive. He was inventing more than absorbing.
At
the end of that year, just before the winter solstice, a comet appeared low in
the sky, its mysterious tail blazing toward the west. Newton stayed outdoors
night after night, noting a path against the background of the fixed stars,
watching till it vanished in the light of each dawn, and only then returned to
his room, sleepless and disordered. A comet was a frightening portent, a
mutable and irregular traveler through the firmament. Nor was that all: rumors
were reaching England of a new pestilence in Holland perhaps from Italy or the Levant,
perhaps from Crete or Cyprus.
Hard behind the
rumors came the epidemic. Three men in London succumbed in a single house; by
January the plague, this disease of population density, was spreading from
parish to parish, hundreds dying each week, then thousands. Before the outbreak
ran its course, in little more than a year, it killed one of every six
Londoners. Newton's mother wrote from Woolsthorpe:
Isack
received your leter
and I perceive you letter from me with your cloth but none to you your sisters
present thai love to you with my motherly lov you and prayers to god for you I
your loving mother
hanah
wollstrup may the
6. 16654
The
colleges of Cambridge began shutting down. Fellows and students dispersed into
the countryside.
Newton
returned home. He built bookshelves and made a small study for himself. He
opened the nearly blank thousand‑page commonplace book he had inherited
from his stepfather and named it his Waste Book.' He began filling it with
reading notes. These mutated seamlessly into original research. He set himself
problems; considered them obsessively; calculated answers, and asked new
questions. He pushed past the frontier of knowledge (though he did not know
this). The plague year was his transfiguration. Solitary and almost incommunicado, he became the world's
paramount mathematician.
Most of the
numerical truths and methods that people had discovered, they had forgotten and
rediscovered, again and again, in cultures far removed from one another.
Mathematics was evergreen. One scion of Homo sapiens could still comprehend virtually all that the species knew
collectively. Only recently had this form of knowledge begun to build upon
itself. Greek mathematics had almost
vanished; for centuries, only Islamic mathematicians had kept it alive,
meanwhile inventing abstract methods of problem solving called algebra. Now
Europe became a special case: a region where people were using books and mail
and a single language, Latin, to span tribal divisions across hundreds of
miles; and where they were, self‑consciously, receiving communications
from a culture that had flourished and then disintegrated more than a thousand
years before. The idea of knowledge as cumulative ‑ a ladder, or a tower
of stones, rising higher and higher ‑ existed only as one possibility
among many. For several hundred years, scholars of scholarship had considered
that they might be like dwarves seeing farther by standing on the shoulders of
giants, but they tended to believe more in rediscovery than in progress. Even
now, when for the first time Western mathematics surpassed what had been known
in Greece, many philosophers presumed they were merely uncovering ancient
secrets, found in sunnier times and then lost or hidden.
With printed books
had come a new metaphor for the world's organization. The book was a container
for information, designed in orderly patterns, encoding the real in symbols;
so, perhaps, was nature itself. The book
of nature became a favorite conceit of philosophers and poets: God had
written; now we must read. "Philosophy is written in this grand book ‑
I mean the universe ‑ which stands continually open to our gaze,"
said Galileo. "But the book cannot be understood unless one first learns
to comprehend the language and read the letters in which it is composed. It is
written in the language of mathematics....
But by mathematics
he did not mean numbers: "Its characters are triangles, circles, and other
geometrical figures, without which it is humanly impossible to understand a
single word of it; without these, one is wandering about in a dark
labyrinth."
The study of
different languages created an awareness of language: its arbitrariness, its
changeability. As Newton learned Latin and Greek, he experimented with
shorthand alphabets and phonetic writing, and when he entered Trinity College
he wrote down a scheme for a "universal" language, based on
philosophical principles, to unite the nations of humanity. "The Dialects
of each Language being soe divers & arbitrary," he declared, "a
generall Language cannot bee so fitly deduced from them as from the natures of
things themselves." He understood language as a process, an act of
transposition or translation ‑ the conversion of reality into symbolic
form. So was mathematics, symbolic translation at its purest.
For a lonely
scholar seeking his own path through tangled thickets, mathematics had a
particular virtue. When Newton got answers, he could usually judge whether they
were right or wrong, no public disputation necessary. He read Euclid carefully
now. The Elements ‑ transmitted
from ancient Alexandria via imperfect Greek copies, translated into
medieval Arabic, and translated again into Latin – taught him the fundamental
program of deducing the properties of triangles, circles, lines, and spheres
from a few given axioms. He absorbed
Euclid's theorems for later use, but he was inspired by the leap of Descartes's
Geometrie, a small and rambling text,
the third and last appendix to his Discours
de la Methode. This forever joined two great realms
of thought, geometry and algebra. Algebra (a "barbarous" art,
Descartes said, but it was his subject none theless) manipulated unknown
quantities as if they were known, by assigning them symbols. Symbols recorded
information, spared the memory, just as the printed book did. Indeed, before texts could spread by
printing, the development of symbolism had little point.
With symbols came
equations: relations between quantities, and changeable relations at that. This
was new territory, and Descartes exploited it. He treated one unknown as a
spatial dimension, a line; two unknowns thus define a plane. Line segments
could now be added and even multiplied. Equations generated curves; curves
embodied equations. Descartes opened the cage doors, freeing strange new
bestiaries of curves, far more varied than the elegant conic sections studied
by the Greeks. Newton immediately began expanding the possibilities, adding
dimensions, generalizing, mapping one plane to another with new coordinates. He
taught himself to find real and complex roots of equations and to factor
expressions of many terms‑polynomials. When the infinite number of points
in a curve correspond to the infinite solutions of its equation, then all the
solutions can be seen at once, as a unity. Then equations have not just solutions
but other properties: maxima and minima, tangents and areas. These were
visualized, and they were named.
No
one understands the mental faculty we call mathematical intuition; much less,
genius. People's brains do not differ much, from one to the next, but numerical
facility seems rarer, more special, than other talents. It has a threshold
quality. In no other intellectual realm does the genius find so much common
ground with the idiot savant. A mind turning inward from the world can see
numbers as lustrous creatures; can find order in them, and magic; can know
numbers as if personally. A mathematician, too, is a polyglot. A powerful
source of creativity is a facility in translating, seeing how the same thing
can be said in seemingly different ways. If one formulation doesn't work, try
another.

Newton's patience
was limitless. Truth, he said much later, was "the offspring of silence
and meditation."
And he said:
"I keep the subject constantly before me and wait 'till the first dawnings
open slowly, by little and little, into a full and clear light."
Newton's Waste Book
filled day by day with new research in this most abstract of realms. He
computed obsessively. He worked out a way to transform equations from one set
of axes to any alternative frame of reference. On one page he drew a hyperbola
and set about calculating the area under it ‑ "squaring" it. He
stepped past the algebra Descartes knew. He would not confine himself to
expressions of a few (or many) terms; instead he constructed infinite series:
expressions that continue forever. An
infinite series need not sum to infinity; rather, because the terms could grow
smaller and smaller, they could close in on a goal or limit. He conceived such
a series to square the hyperbola‑
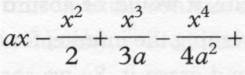
‑and
carried out the calculation to fifty‑five decimal places: in all, more
than two thousand tiny digits marching down a single page in orderly
formation. To conceive of infinite
series and then learn to manipulate them was to transform the state of mathematics.
Newton seemed now to possess a limitless ability to generalize, to move from
one or a few particular known cases to the universe of all cases.
Mathematicians had a glimmering notion of how to raise the sum of two
quantities, a + b, to some power. Through infinite series, Newton discovered in
the winter of 1664 how to expand such sums to any power, integer or not: the
general binomial expansion.

He relished the
infinite., as Descartes had not. "We should never enter into arguments
about the infinite," Descartes had written.
For since we are finite, it would be absurd for us to determine
anything concerning the infinite; for this would be to attempt to limit it and
grasp it. So we shall not bother to reply to those who ask if half an infinite
line would itself be infinite, or whether an infinite number is odd or even,
and so on. It seems that nobody has any business to think about such matters
unless he regards his own mind as infinite.
Yet it turns out that the human
mind, though bounded in a nutshell, can discern the infinite and take its
measure.
A special aspect of
infinity troubled Newton; he returned to it again and again, turning it over,
restating it with new definitions and symbols. It was the problem of the
infinitesimal ‑ the quantity, impossible and fantastic, smaller than any
finite quantity, yet not so small as zero. The infinitesimal was anathema to
Euclid and Aristotle. Nor was Newton altogether at ease with it. First he thought in terms of "indivisibles"‑points
which, when added to one another infinitely, could perhaps make up a finite
length. This caused paradoxes of dividing by zero:
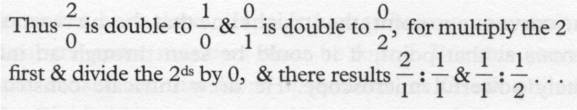
‑nonsensical results if 0 is truly
zero, but necessary if 0 represents some indefinitely small.,
"indivisible" quantity. Later he added an afterthought‑
Tis indefinite (that is undetermined) how greate a sphxre may be made how greate
a number may be reckoned, how far matter is divisible, how much time or
extension wee can fansy but all the Extension that is, Eternity, a /0 are
infinite.
‑blurring the words indefinite and undetermined by applying them alternately to mathematical
quantities and degrees of knowledge. Descartes's reservations notwithstanding,
the infinitude of the universe was in play – the boundlessness of God's space and time. The infinitesimal ‑
the almost nothing ‑ was another matter. It might have been simply the
inverse problem: the infinitely large and the infinitely small. A star of
finite size, if it could be seen at an infinite distance, would appear
infinitesimal. The terms in Newton's infinite series approached the
infinitesimal. "We are among infinities and indivisibles," Galileo
said, "the former incomprehensible to our understanding by reason of their
largeness, and the latter by their smallness."
Newton was seeking better methods‑more
general‑for finding the slope of a curve at any particular point, as well
another quantity, related but once removed, the degree of curvature, rate of
bending, "the crookedness in lines."
He applied himself to the tangent, the straight line that grazes the
curve at any point, the straight line that the curve would become at that point, if it could be seen through an infinitely
powerful microscope. He drew intricate constructions, more complex and more
free than anything in Euclid or Descartes. Again and again he confronted the
specter of the infinitesimal: "Then (if hs & cd have an infinitely
little distance otherwise not) . “;”. . (which operacon cannot in this case bee
understood to bee good unlesse infinite littleness may bee considered geometrically)
...”. He could not escape it, so he
pressed it into service, employing a private symbol ‑ a little o ‑
for this quantity that was and was not zero. In some of his diagrams, two
lengths differed "but infinitely little," while two other lengths had
"no difference at all." It was essential to preserve this uncanny
distinction. It enabled him to find areas by infinitely partitioning curves and
infinitely adding the partitions. He created "a Method whereby to square
those crooked lines which may bee squared" ‑ to integrate (in the later language of the calculus).
As algebra melded
with geometry, so did a physical counterpart, the problem of motion. Whatever
else a curve was, it naturally represented the path of a moving point. The
tangent represented the instantaneous direction of motion. An area could be
generated by a line sweeping across the plane. To think that way was to think
kinetically. It was here that the infinitesimal took hold. Motion was smooth,
continuous, unbroken‑how could it be otherwise? Matter might reduce to
indivisible atoms, but to describe motion, mathematical points seemed more
appropriate. A body on its way from a to b
must surely pass through every point between. There must be points between, no matter how close a
is to b; just as between any pair of
numbers, more numbers must be found. But this continuum evoked another form of
paradox, as Greek philosophers had seen two thousand years before: the paradox
of Achilles and the tortoise. The tortoise has a head start. Achilles can run
faster but can never catch up, because each time he reaches the tortoise's last
position, the tortoise has managed to crawl a bit farther ahead. By this logic
Zeno proved that no moving body could ever reach any given place ‑ that
motion itself did not exist. Only by embracing the infinite and the
infinitesimal, together, could these paradoxes be banished. A philosopher had
to find the sum of infinitely many, increasingly small intervals. Newton
wrestled with this as a problem of words: swifter, slower; least distance,
least progression; instant, interval.
That it may be knowne how motion is swifter or slower consider: that
there is a least distance, a least progression in motion & a least degree
of time.... In each degree of time wherein a thing moves there will be motion
or else in all those degrees put together there will be none: ... no motion is
done in an instant or intervall of time.
A culture lacking
technologies of time and speed also lacked basic concepts that a mathematician
needed to quantify motion. The English language was just beginning to adapt its
first unit of velocity: the term knot, based
on the sailor's only speed‑measuring device, the log line heaved into the
sea. Ile science most eager to understand the motion of earthly objects,
ballistics, measured the angles of gun barrels and the distances their balls
traveled, but scarcely conceived of velocity; even when they could define this
quantity, as a ratio of distance and time, they could not measure it. Galileo,
when he dropped weights from towers, could make only the crudest estimates of
their velocity, though he used an esoteric unit of time: seconds of an hour. Newton was struck by the ambition in his
exactitude: "According to Galileo an iron ball of 100 lb. Florentine (that
is 78 lb. at London avoirdupois weight) descends 100 Florentine braces or
cubits (or 49.01 Ells, perhaps 66 yds.) in 5 seconds of an hour.”
In the autumn of
1665 he made notes on "mechanical" lines, as distinguished from the
merely geometric. Mechanical curves were those generated by the motion of a
point, or by two such motions compounded: spirals, ellipses, and cycloids.
Descartes had considered the cycloid, the curve generated by a point on a
circle as the circle rolls along a line. He regarded this oddity as suspect and
unmathematical, because it could not (before the calculus) be described
analytically. But such artifacts from the new realm of mechanics kept intruding
on mathematics. Hanging cables or sails in the wind traced mechanical curves.
If a cycloid was mechanical, it was nevertheless an abstraction: a creature of
several motions, or rates, summed in a certain way. Indeed, Newton now saw
ellipses in different lights – geometrical and analytical. The ellipse was the
effect of a quadratic formula. Or it was the closed line drawn in the dirt by
the "gardener's" construction, in which a loose cord is tied to two
pegs in the ground: "keeping it so stretched out draw the point b about & it shall describe the
Ellipsis.” Or it was a circle with
extra freedom; a circle with one constraint removed; a squashed circle, its
center bifurcating into a pair of foci. He devised procedures for drawing
tangents to mechanical curves, thus measuring their slopes; and, in November,
proposed a method for deducing, from two or more such lines, the corresponding
relation between the velocities of two or more moving bodies.
He found tangents
by computing the relationship between points on a curve separated by an
infinitesimal distance. In the computation, the points almost merge into one,
" conjoyne, which will happen when bc
= 0, vanisheth into nothing." That o was an artifice, a gadget for the
infinitesimal, as an arbitrarily small increment or a moment of time. He showed
how the terms with o "may be ever blotted out.” Extending his methods, he also quantified rates of bending, by
finding centers of curvature and radii of curvature.
A geometrical task
matched a kinetic task: to measure curvature was to find a rate of change. Rate of change was itself an abstraction
of an abstraction; what velocity was to position, acceleration was to velocity.
It was differentiation (in the later language of the calculus). Newton saw this
system whole: that problems of tangents were the inverse of problems of
quadrature; that differentiation and integration are the same act, inverted.
The procedures seem alien, one from the other, but what one does, the other
undoes. That is the fundamental theorem of the calculus, the piece of
mathematics that became essential knowledge for building engines and measuring
dynamics. Time and space‑joined. Speed
and area ‑ two abstractions,
seemingly disjoint, revealed as cognate.
Repeatedly he
started a new page ‑ in November 1665, in May 1666, and in October 1666 ‑
in order to essay a system of propositions needed "to resolve Problems by motion. " On his last attempt he produced
a tract of twenty four pages, on eight sheets of paper folded and stitched
together. He considered points moving toward the centers of circles; points
moving parallel to one another; points moving "angularly" or
"circularly" ‑ this language was unsettled ‑ and points
moving along lines that intersected planes. A variable representing time
underlay his equations‑time as an absolute background for motion. When
velocity changed, he imagined it changing smoothly and continuously ‑
across infinitesimal moments, represented by that o. He issued himself
instructions:
Set all the termes on one side of the Equation that they become equall
to nothing. And first multiply each terme by so many times p / x as x hath dimensions in the terme. Secondly
multiply each term by so many times q /
y there bee still more unknowne quantitys doe like to every unknowne quantity.
Time was a flowing thing. In terms of velocity, position was a function
of time. But in terms of acceleration, velocity was itself a function of time.
Newton made up his own notation, with combinations of superscript dots, and
vocabulary, calling these functions "fluents" and
"fluxions": flowing quantities and rates of change. He wrote it all
several times but never quite finished.
In creating this
mathematics Newton embraced a paradox. He believed in a discrete universe. He
believed in atoms, small but ultimately indivisible ‑ not infinitesimal.
Yet he built a mathematical framework that was not discrete but continuous,
based on a geometry of lines and smoothly changing curves. "All is flux,
nothing stays still," Heraclitus had said two millennia before.
"Nothing endures but change." But this state of being ‑ in
flow, in change ‑ defied mathematics then and afterward. Philosophers
could barely observe continuous change, much less classify it and gauge it,
until now. It was nature's destiny now to be mathematized. Henceforth space
would have dimension and measure; motion would be subject to geometry.
Far away across the country multitudes were dying in fire and plague.
Numerologists had warned that 1666 would be the Year of the Beast. Most of
London lay in black ruins: fire had begun in a bakery, spread in the dry wind
across thatch‑roofed houses, and blazed out of control for four days and
four nights. The new king, Charles II ‑ having survived his father's
beheading and his own fugitive years, and having outlasted the Lord Protector,
Cromwell ‑ fled London with his court. Here at Woolsthorpe the night was
strewn with stars, the moon cast its light through the apple trees, and the
day's sun and shadows carved their familiar pathways across the wall. Newton
understood now: the projection of curves onto flat planes; the angles in three
dimensions, changing slightly each day. He saw an orderly landscape. Its
inhabitants were not static objects; they were patterns, process and change.
What he wrote, he
wrote for himself alone. He had no reason to tell anyone. He was twenty‑four
and he had made tools.
Chapter
4 Two Great Orbs
Historians
came to see Newton as an end‑point: the "culmination" and
"climax" of an episode in human affairs conventionally called the Scientific
Revolution. Then that term began to require apologies or ironic quotation
marks. Ambivalence is appropriate, when
one speaks of the turning point in the development of human culture, the time
when reason triumphed over unreason. The Scientific Revolution is a story, a
narrative frame laid down with hindsight. Yet it exists and existed, not just
in the backward vision of historians but in a self‑consciousness among a
small number of people in England and Europe in the seventeenth century. They
were, as they thought, virtuosi. They saw something new in the domain of
knowledge; they tried to express the newness; they invented academies and
societies and opened channels of communication to promote their break with the
past, their new science.
We call the
Scientific Revolution an epidemic, spreading across the continent of Europe
during two centuries: "It would come to rest in England, in the person of
Isaac Newton," said the physicist David Goodstein. "On the way north,
however, it stopped briefly in France. . . ." Or a relay race, run by a
team of heroes who passed the baton from one to the next: COPERNICUS to KEPLER
to GALILEO to NEWTON. Or the overthrow and destruction of the Aristotelian
cosmology: a worldview that staggered under the assaults of Galileo and
Descartes and finally expired in 1687, when Newton published a book.
For so long the
earth had seemed the center of all things. The constellations turned round in
their regular procession. just a few bright objects caused a puzzle‑the
planets, wanderers, like gods or messengers, moving irregularly against the
fixed backdrop of stars. In 1543, just before his death, Nicolaus Copernicus,
Polish astronomer, astrologer, and mathematician, published the great book De Revolutionibus Orbium Coelestium ("On
the Revolutions of the Heavenly Spheres"). In it he gave order to the
planets' paths, resolving them into perfect circles; he set the earth in motion
and placed an immobile sun at the center of the universe.
Johannes Kepler,
looking for more order in a growing thicket of data, thousands of painstakingly
recorded observations, declared that the planets could not be moving in
circles. He suspected the special curves known to the ancients as ellipses.
Having thus overthrown one kind of celestial perfection, he sought new kinds,
believing fervently in a universe built on geometrical harmony. He found an
elegant link between geometry and motion by asserting that an imaginary line
from a planet to the sun sweeps across equal areas in equal times.
Galileo Galilei took spy‑glasses‑made
by inserting spectacle makers' lenses into a hollow tube‑and pointed them
upward toward the night sky. What he saw both inspired and disturbed him: moons
orbiting Jupiter; spots marring the sun's flawless face; stars that had never
been seen ‑ "in numbers ten times exceeding the old and familiar
stars.” He learned, "with all the
certainty of sense evidence," that the moon "is not robed in a smooth
polished surface but is in fact rough and uneven." It has mountains,
valleys, and chasms. (He also thought he had detected an atmosphere of dense
and luminous vapors.)
He took pains to
detail an unfamiliar fact of arithmetic: that, because in his spy‑glass
the moon's diameter appeared thirty times larger, its apparent area was
magnified by 900 and its apparent volume by 27,000 ‑ a square law and a
cube law. This was essentially the only mathematics in his report, The Starry Messenger.
It was strange to
think of these dots of light as worlds, and more strange to think of a world‑the
whole world‑as a body in
motion, comparable to a mere stone. Yet without understanding motion, no one
could place the heavenly bodies. There could be no cosmology without dynamics.
Galileo felt this. What he saw in the skies of Florence in 1610, English
pamphleteers tried to convey a generation later. In London a young chaplain,
John Wilkins, began writing anonymous screeds. First, in 1638, The Discovery of a New World; or, a
Discourse tending to prove, that it is probable there may be another habitable
World in the Moon.
Among all the
celestial mysteries, the moon was special‑so near, so changeling, so
portentous. It stirred madness in weak minds; people were known to grow lunatic
on a monthly cycle. Empedocles saw the moon as "a globe of pure congealed
air, like hail inclosed in a sphere of fire." Aristotle held it to be
solid and opaque, whereas Julius Caesar said it must be transparent and pure,
of the same essence as the heavens. Plain observation, night after night,
failed to settle such matters. "You may as soon persuade some country
peasants that the moon is made of green cheese (as we say) as that it is bigger
than his cart‑wheel," wrote Wilkins, "since both seem equally
to contradict his sight, and he has not reason enough to lead him farther than
his senses."
How far could
reason lead, without help? Francis Bacon, who had practiced logic and
disputation as the king's Learned Counsel and Attorney‑General, lamented
a natural philosophy built solely on words, ostentation, the elaborate knitting
together of established ideas.
All the philosophy of nature
which is now received, is either the philosophy of the Grecians, or that other
of the alchemists. . . . The one is gathered out of a few vulgar observations,
and the other out of a few experiments of a furnace. The one never faileth to
multiply words, and the other ever faileth to multiply gold.
He
argued for experiment‑the devising of "Crucial Instances" to
divide the true from the false. Was the moon flame‑like and airy or solid
and dense? Since the moon reflects the sun's light, Bacon proposed, a crucial
instance would be a demonstration that a flame or other rare body does or does
not reflect light. Perhaps the moon also "raises the waters," Bacon
suggested, and "makes moist things swell." He proposed to call this
effect Magnetic Motion."
Wilkins cited the
lunar observations of many authorities: Herodotus, the venerable Bede, the
Romish divines, the Stoics, Moses, and Thomas Aquinas. But at last he chose a
new witness.
I shall most insist on the observation of Galilaeus, the inventor of
that famous perspective, whereby we may discern the heavens hard by us; whereby
those things which others have formerly guessed at, are manifested to the eye,
and plainly discovered beyond exception or doubt.
With his glass,
Galileo could see plainly at a distance of sixteen miles what the naked eye
could scarcely see at a mile and a half. He saw mountains and valleys; he saw a
sphere of thick vaporous air; from these it was but a short step to infer wind
and rain, seasons and weather, and so, Wilkins concluded, inhabitants. "Of
what kind they are, is uncertain," he conceded. "But I think that
future ages will discover more; and our posterity, perhaps, may invent some
means for our better acquaintance with these inhabitants." As soon as the
art of flying is discovered, he said, we should manage to transplant colonies
to that other world. After all, time is the father of truth; ages passed before
men crossed the seas and found other men at the far side of the world; surely
other excellent mysteries remain to be discovered.
Wilkins urged that
the strangeness of his opinions should be no reason to reject them. The
surprising discovery of another New World weighed heavily: "How did the
incredulous gaze at Columbus, when he promised to discover another part of the
earth?"
Still, he agreed
that the idea of multiple worlds brought paradoxical difficulties. 'Me most
troublesome was the tendency of heavy bodies to fall down: their gravity.
"What a huddling and confusion must there be, if there were two places for
gravity and two places for lightness?"
Which way should bodies of that other world fall? To where should its
air and fire ascend? Can we expect pieces of the moon to fall to earth?
He answered these
questions in the terms of Copernicus and Kepler: by proposing that two worlds
must have two centers of gravity. "There is no more danger of their
falling into our world, than there is fear of our falling into the moon."
He reminded his readers of the simple nature of gravity: "nothing else,
but such a quality as causes a propension in its subject to tend downwards
towards its own centre."
The discovery of
new worlds had lit a fuse leading to the destruction of the Aristotelian
conception of gravity. It was inevitable. A multitude of worlds implied a
multitude of reference frames. Up and down became relative terms, in the
imaginations of philosophers, contrary to common experience. Wilkins did not
shrink from considering the problem of what would happen to an object ‑ a
bullet, perhaps ‑ sent to such a great height that it might depart
"that magnetical globe to which it did belong." It might just come to
rest, he decided. Outside the earth's sphere of influence, pieces of earth
should lose their gravity, or their susceptibility to gravity. He offered a
"similitude":
As any light body (suppose the sun) does send forth its beams in an
orbicular form; so likewise any magnetical body, for instance a round
loadstone, does cast abroad his magnetical vigour in a sphere.... Any other
body that is like affected coming within this sphere will presently descend
towards the centre of it, and in that respect may be styled heavy. But place it
without this sphere, and then the desire of union ceaseth, and so consequently
the motion also.
Newton read Wilkins
as a boy in Grantham, at the apothecary Clarke's. Whatever else he thought
about the moon, he knew it was a great planetary object traveling through space
at high speed. The mystery was why. Carried along, as Descartes said, in a
vortex? Newton knew how big the moon was and how far away. By virtue of a
coincidence, the moon's apparent size was almost exactly the same as the sun's,
about one‑half degree of arc, the coincidence that makes a solar eclipse
such a perfect spectacle. It was necessary now to forge mental links across
many orders of magnitude in scale: between the everyday and the unimaginably
vast. Sitting in the orchard behind his farmhouse, musing continually on
geometry, Newton could see other globes, dangling from their stems. A two‑inch
apple at a distance of twenty feet subtended the same half‑degree in the
sky. These ratios were second nature
now, the congruent Euclidean triangles inscribed in his mind's eye. When he
thought about the magnitude of these bodies, another automatic part of the
picture was an inverse square law: something varies as 1/X2. A disk
twice as far away would seem not one‑half as bright but one‑fourth.
Newton was eager,
as the Greeks had not been, to extend the harmony and abstraction of
mathematics to the crude sublimary world in which he lived. An apple was no
sphere, but he understood it to be flying through space along with the rest of
the earth's contents, spinning across 25,000 miles each day. Why, then, did it
hang gently downward, instead of being flung outward like a stone whirled
around on a string? The same question applied to the moon: what pushed it or
pulled it away from a straight path?
Many years later
Newton told at least four people that he had been inspired by an apple in his
Woolsthorpe garden ‑ perhaps an apple actually falling from a tree,
perhaps not. He never wrote of an apple. He recalled only:
I began to think of
gravity extending to the orb of the Moon ...
‑gravity as a
force, then, with an extended field of influence; no cutoff or boundary --
& computed the
force requisite to keep the Moon in her Orb with the force of gravity at the
surface of the earth ... & found them answer pretty nearly. All this was in
the two plague years of 1665‑1666. For in those days I was in the prime
of my age for invention & minded Mathernaticks and Philosophy more than at
any time since.
Voltaire did
mention the apple, as did other memoirists, and their second‑ and third‑hand
accounts gradually formed the single most enduring legend in the annals of
scientific discovery. And the most
misunderstood: Newton did not need an apple to remind him that objects fell to
earth. Galileo had not only seen objects fall but had dropped them from towers and
rolled them down ramps. He had grasped their acceleration and struggled to
measure it. But most emphatically he declined to explain it. "The present
does not seem to be the proper time to investigate the cause of the
acceleration," Galileo wrote, ". . . [but] merely to investigate and
to demonstrate some of the properties of accelerated motion (whatever the
cause of this acceleration may be)."
Nor did Newton
comprehend universal gravitation in a flash of insight. In 1666 he was barely
beginning to understand. What he suspected about gravity he kept private for
decades to come.
The apple was
nothing in itself. It was half of a couple the moon's impish twin. As an apple
falls toward the earth, so does the moon: falling away from a straight line,
falling around the earth. Apple and moon were a coincidence, a generalization,
a leap across scales, from close to far and from ordinary to immense. In his
study and in his garden, in his state of incessant lonely contemplation, his
mind alive with new modes of geometry and analysis, Newton made connections
between distant realms of thought. Still, he was unsure. His computations were
ambiguous; he only found them answer
pretty nearly. He was attempting rare exactitude, more than any available
raw data could support. Even the units of measure were too crude and variable.
He took the mile to be 5,000 feet.20 He set one degree of the earth's latitude
at the equator equal to sixty miles, an error of about 15 percent. Some units
were English, some antique Latin, others Italian: mile, passus, brace, pedes.
He came up with a datum for the speed of the revolving earth: 16,500,000 cubits
in six hours. He struggled to arrive at
a datum for the rate of fall due to gravity. He had Galileo's calculations, in
a new translation: one hundred cubits in five seconds. He tried to derive his own measurements
using a weight hanging on a cord and swinging in circles‑a conical
pendulum. This needed patience. He noted the pendulum making 1,512
"ticks" in an hour. He
arrived at a constant for gravity more than double Galileo's. He concluded that
a body on the earth's surface is drawn downward by gravity 350 times stronger
than the tendency of the earth's rotation to fling it outward.
To make the
arithmetic work at all, he had to suppose that the power of attraction
diminished rapidly according to distance from the center of the earth. Galileo
had said that bodies fall with constant acceleration, no matter how far they
are from the earth; Newton sensed that this must be wrong. And it would not be
enough for gravity to fade in proportion to distance. He estimated that the
earth attracted an apple 4,000 times as powerfully as it attracted the distant
moon. If the ratio‑like brightness, and like apparent area ‑
depended on the square of distance,
that Might answer pretty nearly.
He reckoned the
distance of the moon at sixty times the earth's radius; if the moon were sixty
times farther than the surface of the earth from the center of the earth, then
the earth's gravity might be 3,600 times weaker there. He also derived this
inverse‑square law by an inspired argument from an observation of
Kepler's: the time a planet takes to make one orbit grows as the 3/2 power of
its distance from the sun. Yet, with
the data he had, he could not quite make the numbers work. He still found it
necessary to attribute some of the moon's motion to the vortices of Descartes.
He needed new
principles of motion and force. He had tried some out in the Questiones, and now, in the plague year,
he tried again. He wrote " axioms" in the Waste Book:
1. If a quantity
once move it will never rest unlesse hindered by some externall caus.
2. A quantity will
always move on in the same streight line (not changing the determination nor
celerity of its motion) unless some externall cause divert it.
Thus circular
motion‑orbital motion‑demanded explanation. So far, the external cause was missing from the
picture. And Newton posed himself a challenge: it ought to be possible to
quantify this cause.
3. There is exactly
so much required so much and noe more force to reduce a body to rest as there
was to put it upon motion.
He continued
through dozens more axioms, comprising a logical whole, but a tangled one. He
was hampered by the chaos of language ‑ words still vaguely defined and
words not quite existing. He conceived offorce as a thing to be measured ‑
but in what units? Was force inherent in bodies, as Descartes thought? Or was
force an external agent, impinging on bodies and changing a differently named
quantity: quantity of motion; or quantity of mutation in its state; or whole motion; or force of motion? Whatever this missing concept
was, it differed from velocity and direction. Axiom 100:
A
body once moved will always keepe the same celerity, quantity and determination
of its motion.
At twenty‑four,
Newton believed he could marshal a complete science of motion, if only he could
find the appropriate lexicon, if only he could set words in the correct order.
Writing mathematics, he could invent his own symbols and form them into a mosaic.
Writing in English, he was constrained by the language at hand. At times his frustration was palpable in the
stream of words. Axiom 103:
... as the body (a) is to the body (b) so must the power or efficacy
vigor strength or virtue of the cause which begets the same quantity of
velocity ....
Power efficacy
vigor strength virtue‑‑‑something
was missing. But these were the laws of motion, in utero.
Chapter
5 Bodys & Senses
He
was looking inward as well as outward. Introspection told him that his imagination
could see things as they really were. "Phantasie is helped," he
noted, "by good' aire fasting moderate wine." But it is also
"spoiled by drunkenesse, Gluttony, too much study." He added: from
too much study, and from extreme passion, "cometh madnesse."
He wished to
understand light itself‑but did light's essence lie outside or within the
soul of the observer? In all the blooming perplexity of new philosophy, little
was as muddled as the boundary between the perceived and the perceiver. Surely
the mind, composed of pure thought, must have a point of contact with the body‑at
the pineal gland, Descartes proposed. The poet Andrew Marvell, graduate of
Trinity College and now Member of Parliament for Hull, imagined the body and
soul as enslaved, each by the other: "A soul hung up, as 'twere, in chains
of nerves and arteries and veins.” For
Aristotle optics had been first a science not of light but of sight.
Newton, in his Questiones, had pondered the difficulty
of understanding the senses, when those very senses were employed as the agents
of understanding.
The nature of things is more securely & naturally deduced from
their operations out upon another than upon our senses. And when by the former
experiments we have found the nature of bodys, by the latter we may more
clearely find the nature of our senses. But so long as we are ignorant of the
nature of both soul and body we cannot clearly distinguish how far an act of
sensation proceeds from the soul and how far from the body.
With this paradox in mind, Newton, experimental philosopher, slid a
bodkin into his eye socket between eyeball and bone. He pressed with the tip
until he saw "severall white darke & coloured circles .... Which
circles were plainest when I continued to rub my eye with the point of the
bodkin." Yet when he held both eye and bodkin still, the circles would
begin to fade. Was light a manifestation of pressure, then?

Almost as
recklessly, he stared with one eye at the sun, reflected in a looking glass,
for as long as he could bear. He sensed that color‑perhaps more than any
of the other qualities of things
depends on "imagination and fantasy and invention." He looked away at
a dark wall and saw circles of color.
There was a
"motion of spirits" in his eye. These slowly decayed and finally
vanished. Were they real or phantasm? Could such colors ever be real, like the colors e had learned to
make from crushed be ries or sheep's blood? After looking at the sun, he seemed
to perceive light objects as red and dark objects as blue. Strangely, he found
that he could reproduce these effects, with practice, by pure, willful thought.
"As often as I went into the dark & intended my mind upon them as when
a man looks earnestly to see any thing which is difficult to be seen, I could
make the phantasm return without looking any more upon the sun.” He repeated the experiment until he began to
fear permanent damage and shut himself up in a dark room. He remained there for
three days; only then did his sight begin to clear.
Experiment‑observation‑science:
these modern words were impressing themselves upon him. He read them in a new
book from London, titled Micrographia: "The
Science of Nature has been already too long made only a work of the Brain and
the Fancy. It is now high time that it should return to the plainness and
soundness of Observations on material and obvious things. The author was Robert Hooke, a brilliant and
ambitious man seven years Newton's senior, who wielded the microscope just as
Galileo had the telescope. These were the instruments that penetrated the
barrier of scale and opened a view into the countries of the very large and the
very small. Wonders were revealed there. The old world‑the world of
ordinary scales‑shrank into its place in a continuum, one order among
many. Like Galileo, Hooke made meticulous drawings of strange new sights and
popularized his instrument as a curiosity for wealthy aristocrats‑though,
after they bought the device from the lens shop in London where he sometimes
worked, they rarely succeeded in seeing anything but vague shadows. Hooke was
Newton's inspiration now (though Newton never acknowledged that). He became
Newton's goad, nemesis, tormentor, and victim.
Hooke had a unique
post. He was employed, if seldom actually paid, as Curator of Experiments to a
small group of men who formed, in 1662, what they called the Royal Society of
London. They meant to be a new sort of institution: a national society
dedicated to promoting‑and especially “communicating" ‑ what
they called "the New Philosophy" or "Experimental
Philosophy." Amazing discoveries
warranted this banner: comets and new stars; the circulation of the blood; the
grinding of glasses for telescopes; the possibility of vacuities (and nature's
abhorrence thereof); the descent of heavy bodies; and diverse other things.
Nullius in verba
was the Royal Society's motto. Don't
take anyone's word for it. These
gentlemen had begged for and received the king's patronage, but patronage meant
good will only; the society collected from its members a shilling at a time and
strained to find meeting places. Among the founders was John Wilkins, author of
The Discovery of a New World a
generation before. If one man was their muse, he was the late Francis Bacon,
who had written:
We must ... completely resolve and separate Nature, not by fire,
certainly, but by the mind, which is a kind of divine fire.... There will
remain, all volatile opinions vanishing into smoke, the affirmative form,
solid, true and well defined. Now this is quickly said, but it is only reached
after many twists and turns.
The twists and
turns became the responsibility of the Curator of Experiments, Hooke,
technician and impresario. He demonstrated experiments with air‑pumps. At
one meeting he cut open the thorax and belly of a living dog, observed its
beating heart, and used a bellows to inflate its lungs in an experiment on
respiration, which he later felt reluctant to repeat "because of the
torture of the creature." Another
meeting dazzled and confused the Duchess of Newcastle with colors, magnets,
microscopes, roasted mutton, and blood.
This was all science, a new spirit and almost a method: persuasion from
practical experience, and formalized recording of data. Hooke lacked
mathematics but not ingenuity. He invented or improved barometers,
thermometers, and wind gauges, and he tracked London weather obsessively.
In Micrographia he displayed the "new
visible world" to be seen through the instrument he described as an
artificial organ. "By the help of Microscopes, there is nothing so small,
as to escape our inquiry" he declared.
As a geometer begins with a mathematical point, he examined the point of
a needle‑perfectly sharp, yet under the microscope, blunt and irregular.
By analogy he suggested that the earth itself, seen from a great enough
distance, would shrink to a scarcely visible speck. More specks were to be
found in printed books: he proceeded to study and draw the mark of a full stop,
the punctuation mark‑again surprisingly rough and irregular, "like a
great splatch of London dirt." He
found wonderment in the edge of a razor and the weft of fine linen. He
discovered shifting, iridescent colors in thin flakes of glass. He knew that
Descartes had seen a rainbow of colors in light passed through a prism or a
water drop, and he compared microscopic rainbows.
And here he made
his book something more than a registry and gazetteer for his new world. He
notified readers that he offered a theory‑a
complete and methodical explanation of light and color. Aristotle had
thought of color as a commingling of black and white. His followers considered
colors fundamental qualities of matter, carried by light into the eye.
Descartes had speculated that color came from globules of light changing speed
when refracted by glass or water. Hooke disputed this and, grandly invoking the
shade of Bacon, turned to experiment: an "Experimentum
Crucis, serving as Guide or Land‑mark." True, Hooke observed, a prism produces
colors when refracting light. But he asserted that refraction was not
necessary. His landmark was the production of color in transparent substances:
"for we find, that the Light in the open Air, either in or out of the Sun‑beams, and within a
Room, either from one or many Windows, produces much the same effect."
Light is born of motion, he argued. "That all
kind offiery burning Bodies have
their parts in motion, I think will be very easily granted me." Sensing
more than he could truly see, he asserted that all luminous bodies are in
motion, perhaps vibrating: sparks, rotting wood, and fish. Further, he
observed, or thought he observed, that two colors were fundamental: blue and
red. They were caused by "an impression on the retina of an oblique and confused pulse of light." Where red
and blue "meet and cross each other," the imperfection generated
"all kinds of greens." And
here his theory ended. "It would be somewhat too long a work for this
place zetetically to examine, and positively to prove, what particular kind of motion it is.... It would be too
long, I say, here to insert the discursive progress by which I inquired after
the properties of the motion of Light....”
Yet all in all he claimed to have explained everything; to have given‑"newly"
given‑the causes capable of explicating all the Phenomena of colours, not
onely of those appearing in the Prisme, Water‑drop, or Rainbow ... but of
all that are in the world, whether they be fluid or solid bodies, whether in
thick or thin, whether transparent, or seemingly opacous.”
Newton
absorbed this bold claim. He had no
microscope and no chance of obtaining one. For that matter, he had no room with
more than one window. He did have a prism. He darkened his study and made a
hole in the window shutter to let in a sunbeam, white light, the purest light,
light with no intrinsic color, philosophers still thought. He performed his own
experiments‑even, he felt, an experimentum
crucis. He noted the results and told no one.
Bacon had also
warned: "God forbid that we should give out a dream of our own imagination
for a pattern of the world."
The plague abating,
Newton returned to Cambridge, where among those he did not tell of his
experiments was the professor of mathematics, Isaac Barrow.
Chapter 6
The Oddest If Not the Most Considerable Detection
Newton’s
status at Trinity improved. In October 1667 the college elected fellows for the
first time in three years: men entitled to wages (two pounds a year), a room,
continuing membership in the academic community, and the use of the library.
Each new fellow swore: "I will embrace the true religion of Christ with
all my soul.. . . I will either set Theology as the object of my studies and
will take holy orders when the time prescribed by these statutes arrives, or I
will resign from the college."' Chastity was expected and marriage
forbidden. Newton bought shoes and cloth for the gown of a bachelor of arts.
Besides his stipend he received small sums from his mother and (very rarely)
from pupils he tutored. He bought a set of old books on alchemy, along with
glasses, a tin furnace, and chemicals: aqua fortis, sublimate, vinegar, white
lead, salt of tartar. With these he
embarked on a program of research more secret than ever.
But he also
continued his mathematical investigations, and he shared some of these with Barrow.
He began to list cubic equations: curves in three dimensions, more various and
complex than the ellipses and hyperbolas of two dimensional mathematics. He
attacked this subject as a classifier, trying to sort all such curves into
species and subspecies. As he had done with the calculus, he approached this
analytic geometry from two directions at once: from the perspective of algebra,
where cubic equations begin with the form x3 + ax2 + bx + c = 0; and from a kinematic
perspective, describing these creatures in terms of their construction, as the
results of points and curves moving through space. He plotted in his notebooks
fifty‑eight distinct species of cubics. He sought ever greater
generality.
Barrow showed him a
new book from London, Logarithmotechnia, by
Nicholas Mercator, a mathematics tutor and member of the Royal Society. It
presented a method of calculating logarithms from infinite series and thus
gave Newton a shock: his own discoveries, rediscovered. Mercator had
constructed an entire book‑a useful book, at that from a few infinite
series. For Newton these were merely special cases of the powerful approach to
infinite series he had worked out at Woolsthorpe. Provoked, he revealed to
Barrow a bit more of what he knew. He drafted a paper in Latin, "On
Analysis by Infinite Series." He also let Barrow post this to another
Royal Society colleague, a mathematician, John Collins, but he insisted on anonymity. Only after
Collins responded enthusiastically did he let Barrow identify him: "I am
glad my friends paper giveth you so much satisfaction. his name is Mr Newton; a
fellow of our College, & very young ... but of an extraordinary genius and
proficiency in these things." It was the first transmission of Newton's
name south of Cambridge.
At long distance,
in messages separated by days or by months, Newton and Collins now engaged in a
dance.
Newton
teased Collins with tantalizing fragments of mathematical insight. Collins
begged for more. Newton delayed and withdrew. A table resolving equations of three
dimensions was "pretty easy and obvious enough," he declared.
"But I cannot perswade my selfe to undertake the drudgery of making
it." Collins bruited some of Newton's handiwork to several other
mathematicians, in Scotland, France, and Italy. He sent books to Newton and
posed questions: for example, how to calculate the rate of interest on an
annuity. Newton sent a formula for that but insisted that his name be withheld
if Collins published it: "For I see not what there is desirable in publick
esteeme, were I able to acquire & maintaine it. It would perhaps increase
my acquaintance, the thing which I cheifly study to decline.” Nonetheless his name was being whispered.
James Gregory, the Scots mathematician, heard it. He was struggling with an
unsolved problem of analytic geometry that he read in new lectures by Barrow.
"I despaire of it my self, and therfor I doe humblie desire it of any els
who can resolve it," he wrote Collins. "I long to see that peece of
Mr Newton which is generallie applied to al curvs."
When Barrow
prepared his lectures for publication, he asked Newton to help him edit the
manuscripts, particularly his Optical
Lectures.' These appeared in 1669, with Barrow's effusive acknowledgment of
"a Man of great Learning and Sagacity, who revised my Copy and noted such
things as wanted correction." Yet Newton knew what Barrow did not: that
the whole project wanted correction. Barrow imagined that color had something
to do with compression and rarification and excitation of light; that red might
be "broken and interrupted by shadowy interstices" while blue
involved "white and black particles arranged alternately." Barrow's protege had already done private
research that rendered these optics obsolete. Anyway, Barrow had ambitions
elsewhere. He was a favorite of the king, hoped for advancement, and thought of
himself more as a theologian than a mathematician. Before the end of the year,
he resigned his post as Lucasian professor, yielding it to Newton, twenty‑seven
years old."
The young professor
gained relative security. He could be removed only for serious crime; the
statutes specified fornication, heresy, and voluntary manslaughter. He was
expected to read a lecture on mathematics (broadly construed) each week during
the academic term and deposit a copy in the university library. But he
disregarded this obligation far more than he fulfilled it. When he did lecture,
students were scarce. Sometimes he read to a bare room or gave up and walked
back to his chambers. The existence of this new professorship reflected a sense
that mathematics was an art useful to the growing nation‑its architects,
tradesmen, and sailors‑but cubic curves and infinite series had no use in
a trade or on a ship. Such mysteries were as recondite as the researches Newton
was beginning to undertake alone in his chambers with his tin crucible.
Instead of
mathematics he chose to lecture on light and color. The invention of telescopes
had spurred intense interest in the properties of light, he noted, yet the
geometers had "hitherto erred." So he proposed to add his own
discoveries "to what my reverend predecessor last delivered from this
Place." He considered the
phenomenon of refraction, the bending of light when it passes from one medium
to another, as from air to glass (lenses being the offspring of refraction and
geometry) ‑ Wearing a professor's gown of scarlet, he stood before the
few students who attended and delivered news: rays of colored light differ from
one another in how sharply they are refracted. Each color has its own degree of
refraction. This was a bare, mathematical claim, with none of the romance or
metaphor that usually ornamented the philosophy of light.
Newton was not just
drawing and calculating; he was also grinding glass and polishing lenses in
difficult, nonspherical curves. Telescope makers had learned to their sorrow
that spherical lenses blurred their images, inevitably, because rays of light
failed to meet at a single point. Also, the larger they made the lenses, the
more they saw rings of unwanted color‑and Newton understood these now.
Ile problem lay not in imperfect craft but in the very nature of white light:
not simple but complex; not pure but mixed; a heterogeneous Mixture of differently reftangible rays. Lenses were after all prisms at their edges.
He tried a new kind of telescope, based on a reflecting mirror instead of a
refracting lens. A big mirror would
gather more light than a small lens‑in proportion to its area, or to the
square of its diameter. The difficulty was a matter of craft: how to polish
metal to the smoothness of glass. With his furnace and putty and pitch he cast
a tin and copper alloy and refined its surface, grinding with all his strength.
In 1669 he had a stubby little tube six inches long and magnifying forty times‑as
much as the best telescopes in London and Italy, and as much as a refracting
telescope ten times longer. He kept it
for two years. He saw the disk of Jupiter with its satellites, and Venus
distinctly homed, like a crescent moon. Then he lent it to Barrow. Barrow
carried it to London, to show his friends at the Royal Society.
Like no institution before it, the Royal Society was born dedicated to
information flow. It exalted communication and condemned secrecy. "So far
are the narrow conceptions of a few private Writers, in a dark Age, from being
equal to so vast a design," its founders declared. Science did not exist‑not
as an institution, not as an activity‑but they conceived it as a public
enterprise. They imagined a global network, an "Empire in Learning."
Those striving to grasp the whole fabric of nature
ought to have their eyes in all parts, and to receive information
from every quarter of the earth, they
ought to have a constant universal intelligence: all discoveries should
be brought to them: the Treasuries of all former times should be laid open
before them.
And
in what language? The society's work included translation, contending with
scores of vernacular dialects in Europe, and even stranger languages were
reported to exist in faraway India and Japan. Latin served for standardization,
but the society's founders explicitly worried about the uses of any language.
Philosophy had mired itself in its own florid eloquence. They sought "not
the Artifice of Words, but a bare knowledge of things." Now it was time
for plain speaking, the most naked expression, and when possible this meant the
language of mathematics.

Words were truant
things, elusive of authorities, malleable and relative. Philosophers had much
work to do merely defining their terms, and words like think and exist and word posed greater challenges than tree and moon. Thomas Hobbes warned:
The light of humane
minds is perspicuous words, but by exact definitions first snuffed, and purged
from ambiguity; reason is the pace.... And, on the contrary, metaphors, and
senseless and ambiguous words are like ignesfatui;
and reasoning upon them is wandering amongst innumerable absurdities.
Galileo, having
observed sunspots through his telescope in 1611, could not report the fact
without entering a semantic thicket:
So long as men were in fact obliged to call the sun "most pure and
most lucid," no shadows or impurities whatever had been perceived in it;
but now that it shows itself to us as partly impure and spotty; why should we
not call it "spotted and not pure"? For names and attributes must be
accommodated to the essence of things, and not the essence to the names, since
things come first and names afterwards.
It
has always been so‑this is the nature of language but it has not always
been equally so. Diction, grammar, and orthography were fluid; they had barely
begun to crystallize. Even proper names lacked approved spelling. Weights and
measures were a hodgepodge. Travelers and mail made their way without addresses, unique names and numbers as
coordinates for places. When Newton sent a letter to the Secretary of the Royal
Society, he directed it To Mr Henry
01denburge at his house about the middle of the old palmail in St Jamses Fields
in Westminster
Oldenburg was an
apostle for the cause of collective awareness‑born Heinrich Oldenburg in
the trading city of Bremen (he was never sure what year), later Henricus, and
now Henry. He had come to England during the Civil War as an envoy on a mission
to Oliver Cromwell. He began corresponding with learned men such as Cromwell's
Latin Secretary, John Milton; Cromwell's brother‑in‑law, John
Wilkins; the young philosopher Robert Boyle; and others soon to be the nucleus
of the Royal Society. Then, as an acquaintance put it, "this Curious
German having well improved himself by his Travels, and ... rubbed his Brains
against those of other People, was ... entertained as a Person of great Merit,
and so made Secretary to the Royal Society." He was a master of languages and the perfect focal point for the
society's correspondence. He employed both the ordinary post and a network of
diplomatic couriers to receive letters from distant capitals, especially Paris
and Amsterdam. In 1665 he began printing and distributing this correspondence
in the form of a news sheet, which he called the Philosophical Transactions. This new creature, a journal of
science, remained Oldenburg's personal enterprise till the end of his
life. He found a printer and stationer
with carriers who could distribute a few hundred copies across London and even
farther.
The news took many
forms. Mr. Samuel Colepress, near Plymouth, reported his observations of the
height and velocity of the daily tides; from March to September, he asserted,
the tides tended to be a foot higher ("perpendicular,
which is always to be understood") in the morning than in the
evening. An author in Padua, Italy,
claimed to have discovered new arguments against the motion of the earth, and a
mathematician there disputed him, citing an experiment by a Swedish gentleman,
who fired shots from "a Canon perpendicular to the Horizon" and
observed whether the balls fell toward the west or the east. Mr. Hooke saw a
spot on the planet Jupiter. A very odd monstrous calf was born in Hampshire. A
newly invented instrument of music arrived: a harpsichord, with gut‑strings.
There were poisonous vipers and drops of poison from Florence. The society
examined the weaving of asbestos‑a cloth said to endure the fiercest fire‑and
models of perpetual motion.
No sooner had the
virtuosi begun to gather than England's poets satirized their fixations and
their questions. Hooke himself made an easy target‑his fantastic world of
fleas and animalcules. The natural philosopher could easily be portrayed as a
preoccupied pedant, and not so easily distinguished from the astrologer and the
alchemist. "Which way the dreadful comet went / In sixty‑four and
what it meant?" asked Samuel Butler (his mockery tinged with wonder).
Whether the Moon be
sea or land
Or charcoal, or a
quench'd firebrand ...
These were their learned
speculations
And all their
constant occupations,
To measure wind,
and weigh the air
And turn a circle
to a square.
In fact, travel and
trade, more than speculation or technology, fueled the society's business;
bits of exotic knowledge came as fellow travelers on ships bearing foreign
goods. Spider webs were seen in faraway Bermuda and 300 foot cabbage trees in
the Caribe Islands. A worthy and
inquisitive gentleman, Captain Silas Taylor of Virginia, reported that the
scent of the wild Penny‑royal could kill Ratle‑Snakes. A German
Jesuit, Athanasius Kircher, revealed secrets of the subterranean world: for
example, that the ocean waters continually pour into the northern pole, run
through the bowels of the earth, and regurgitate at the southern pole.
Far away in
Cambridge Newton inhaled all this philosophical news. He took fervid notes.
Rumors of a fiery mountain: "Batavia one after none was covered with a
black dust heavyer then gold which is thought came from an hill on Java Major
supposed to burne.” Rumors of lunar influence: "Oysters & Crabs are
fat at the new moone & leane at the full." Then in 1671 he heard
directly from the voice of the Royal Society. "Sr," Oldenburg wrote,
"Your Ingenuity is the occasion of this addresse by a hand unknowne to you.
. . . "
He said he wished
to publish an account of Newton's reflecting telescope. He urged Newton to take
public credit. This peculiar historical moment‑the manners of scientific
publication just being born‑was alert to the possibilities of plagiarism.
Oldenburg raised the specter of "the usurpation of foreigners" who
might already have seen Newton's instrument in Cambridge, "it being too
frequent, the new Inventions and contrivances are snatched away from their true
Authors by pretending bystanders.” The
philosophers were proposing Newton for election as a fellow of the society.
Still, there were questions. Some of the skillful examiners agreed that
Newton's tube magnified more than larger telescopes, but others said this was
hard to measure with certainty. Some, ill at ease with the technology,
complained that such a powerful telescope made it difficult "to find the
Object." Meanwhile Hooke told the members privately that he himself had
earlier made a much more powerful tiny telescope, in 1664, just an inch long,
but that he had not bothered to pursue it because of the plague and the fire.
Oldenburg chose not to mention Hooke's claim. Newton wrote back with
conventional false modesty:
I was surprised to see so much care taken about securing an invention
to mee, of which I have hitherto had so little value. And therefore since the
R. Society is pleased to think it worth the patronizing, I must acknowledg it
deserves much more of them for that, then of mee, who, had not the
communication of it been desired, might have let it still remained in private
as it hath already done some yeares.
A fortnight later
he set modesty aside. He wished to attend a meeting, he told Oldenburg
dramatically.
I am purposing them, to be considered of & examined, an accompt of a
Philosophicall discovery which induced me to the making of the said Telescope,
& which I doubt not but will prove much more gratefull then the communication
of that instrument, being in my judgment the oddest if not the most
considerable detection which hath hitherto been made in the operations of
Nature.
And by the way,
what would his duties be, as Fellow of the Royal Society?
Chapter
7 Reluctancy and Reaction
The
Great Court of Trinity College was mostly complete, with a library and stables,
central fountain, and fenced‑in plots of grass. An avenue of newly
planted linden trees lay to the southwest.
Newton occupied a chamber upstairs between the Great Gate and the
chapel. To the west stood a four‑walled court used for the game of
tennis. Sometimes he watched fellows play, and he noticed that the ball could
curve, and not just downward. He understood intuitively why this should be so:
the ball was struck obliquely and acquired spin. "Its parts on that side,
where the motions conspire, must press and beat the contiguous Air more
violently than on the other, and there excite a reluctancy and reaction of the
Air proportionately greater.” He noted
this in passing because he had wondered whether rays of light could swerve the
same way, if they "should possibly be globular bodies" spinning
against the ether. But he had decided against that possibility.
He did not go to
London to appear before the Royal Society after all ‑ not for three more
years ‑ but he did not wait to send Oldenburg his promised account of a
philosophical discovery. He composed a long letter in February 1672, to be read
aloud at a meeting. Within a fortnight Oldenburg had it set in type and printed
in the Transactions, along with a
description of the East Indian coasts and an essay on Music.
Newton's letter
presented both an experiment and a “theory”. Six years before, he wrote, he had
aligned his prism in a sunbeam entering a dark room through a hole in the
window shutter. He expected to see all the colors of the rainbow fanned against
the wall and, indeed, he did‑vivid and intense, a very pleasing
divertissement, he reported. Tlis phenomenon of colors was ancient. As soon as
people had glass‑that is, as soon as they had broken glass‑they noticed the appearance of colors where two
refracting surfaces formed a sharp edge. A carefully formed triangular prism
manifested colors most perfectly. No one knew where the colors came from, but
it had seemed clear enough almost by definition, that a prism somehow creates colors.
Experimentum Crucis: The sunbeam from the window shutter passes through one prism,
separating it into colors; then a beam of colored light passes through a second
prism. The second prism has no further separation to perform: the white light
is a mixture, but the colored beams are pure.
Newton noted a
surprise (or so he claimed): where he would have expected the refracted light
to form a circle on the wall‑all the sun's rays being refracted equally‑instead
he saw an oblong. He tried moving the prism, to see whether the thickness of
the glass made a difference. He tried varying the size of the hole in the
window shutter. He tried a second prism. He measured the distance from the
aperture to the wall (22 feet); the length of the colored oblong (13% inches);
its width (2% inches); and the angles of incidence and refraction, known to be
mathematically linked. He noted that the sun was not a point but a disk, spread
across 31 minutes of arc. 'Me sunbeam was always in motion, and he could
examine it only for moments at a time, but he did not let go of this small
oddity‑this peculiar elongation of the image.
It
led him (or so he reported) to the Experimentum
Crucis ‑ the signpost at a crossroads, the piece of experience that
shows which path to trust. Newton took the high‑plumed phrase from Hooke,
who had adapted it from Bacon. The crucial idea was to isolate a beam of colored light and send that through a
prism. For this he needed a pair of prisms and a pair of boards pierced with
holes. He aligned these and carefully rotated one prism in his hand, directing
first blue light and then red light through the second prism. He measured the
angles: the blue rays, bent slightly more by the first prism, were again
refracted slightly more by the second. Most persuasive, though, was that the
second prism never created new colors or altered the colors shining from the
first prism. Years before, in his earliest speculation, he had asked himself,
"Try if two Prismas the one casting blue upon the other's red doe not
produce a white.” They did not. Blue light stayed blue and red stayed red.
Unlike white (Newton deduced) those colors were pure. "And so the true
cause of the length of that Image was detected," Newton declared triumphantly‑"that
Light consists of Rays differently refrangible." Some
colors are refracted more, and not by any quality of the glass but by their own
predisposition. Color is not a modification of light but an original,
fundamental property.
Above all: white
light is a heterogeneous mixture.
But the most
surprising, and wonderful composition was that of Whiteness. There is no one sort of Rays which alone can exhibit this. 'Tis ever compounded, and to
its composition are requisite all the aforesaid primary Colours, mixed in due
proportion. I have often with Admiration beheld, that all the Colours of the Prisme being made to converge,
and thereby to be again mixed, . . . reproduced light, intirely and perfectly
white.
A prism does not
create colors; it separates them. It takes advantage of their different
refrangibility to sort them out.
Newton's letter was
itself an experiment, his first communication of scientific results in a form
intended for publication. It was meant to persuade. He had no template for such
communication, so he invented one: an autobiographical narrative, step by step,
actions wedded to a sequence of reasoning. He exposed intimate feelings: his
pleasure at the display of colors, his uncertainty, and then above all his
surprise and wonder.
A
prism refracts blue light more than red.
The account was an artifice, stylizing a
process of discovery actually carried out over years, on odd occasions,
sometimes below the level of consciousness and computation. A prism in a pencil‑thin
sunbeam actually makes a smudge of color on a wall, uneven and unstable, its
edges shadowy and fading. He idealized what he described; the image made sense
only because he already knew what he was looking for. He had already seen,
years before, that blue light is bent more than red; he had looked through a
prism at red and blue threads and noted their varying refraction. He also knew
that refracting lenses smeared colors; that was why he had invented a
reflecting telescope.
When Descartes looked at a prism in sunlight, he had seen a circle of
colors, not an oblong. A circle was the shape he expected, and it was tiny,
because he directed his prism's light at nearby paper, not a wall twenty‑two
feet distant. Newton wanted to see the oblong, the spreading; he wanted to
magnify it; he wanted to measure it against his geometrical intuition about
the laws of refraction; he believed in precision and in his ability to
interpret small discrepancies.
Indeed,
he believed in mathematics as the road to understanding, and he said so: that
he expected even the science of colors to become mathematical. And this meant certain. "For what I shall tell
concerning them is not an Hypothesis but most rigid consequence," he
wrote, "not conjectured by barely inferring tis thus because not otherwise
. . . but evinced by the mediation of experiments concluding directly &
without suspicion of doubt." Oldenburg omitted this sentence from the
version he printed.
What was light,
anyway? In this offering of a "theory," Newton chose not quite to
commit himself, but he had a mental picture: a ray of light was a stream of
particles, "corpuscles"‑material substance in motion. Descartes
had effect of thought light was pressure in the ether and color an the rotation
of these ether particles; Hooke objected to that and proposed the notion of
light as a pulse, a vibration of the ether, or a wave, like sound. Newton found
Hooke's theory galling. "Though Descartes may bee mistaken so is Mr
Hook," he wrote privately, in taking notes on his copy of Micrographia. He had a simple argument
against a wave theory: light (unlike sound) does not turn corners. "Why
then may not light deflect from straight lines as well as sounds
&c?" In his notes Newton wrote
of light as globules, traveling at finite speed and impinging on the eye. In
his letter he stuck abstractly to rays. "To determine more absolutely,
what Light is, . . . and by what modes or actions it produceth in our minds the
Phastasms of Colours, is not so easie. And I shall not mingle conjectures with
certainties."
Certainties or not,
Newton's conclusions represented a radical assault on the prevailing
wisdom. For the next four years the Philosophical Transactions boiled with
controversy, month after month: ten critiques of Newton's letter and eleven
counters from Newton. Oldenburg kept assuring him of the society's applause for
his ingenuity and frankness and its concern that the honor of discovery might
be snatched from him and assumed by foreigners. In his role as a clearinghouse for developments in mathematics,
Oldenburg discovered that he could use discoveries by foreigners‑for
example, Gottfried Wilhelm Leibniz in Germany, to pry secret knowledge from
Newton. He grew used to Newton's tantalizing style, always holding gems just
out of reach.
And in fact I know myself how to form a series ...
I cannot proceed
with the explanation of it now ...
I have preferred to
conceal it thus ...
Once this was
known, that other could not long remain hidden from me ...
I have another
method not yet communicated, . . . a convenient, rapid and general solution of
this problem, To draw a geometrical curve
which shall pass through any number of given points. . . . These things are
done at once geometrically with no calculation intervening.... Though at first
glance it looks unrnanageable, yet the matter turns out otherwise. For it ranks
among the most beautiful of all that I could wish to solve.
His mathematics
remained mostly hidden. Regarding light, however, he had exposed himself, and
he regretted it. Hooke continued to attack. As Curator of Experiments Hooke
assured the society that he had already performed these very experiments,
hundreds of times. He was not a little pleased, he said, with the niceness and
curiosity of Newton's observations, but he had to confess that he considered
these arguments a mere hypothesis. He said that his own experiments‑"nay
and even those very expts which he alledged" ‑ proved that light is
a pulse in the ether and A that color is nothing but a disturbance of that
light. He would be glad to see "one Experimenturn crucis from Mr
Newton" to make him change his mind, but this was not it. A prism adds
color to light, he insisted, just as an organ pipe or a violin string adds
sound to the air. A French Jesuit,
Ignace Pardies, wrote from Paris that Newton's "hypothesis" would
overthrow the very basis of optics ‑ that the oblong image could be
explained by rays coming, from different parts of the sun's face; and that
mixing colored rays of light produces only a dark blur, not white.
All this angered
Newton, especially the word hypothesis. He was not offering a hypothesis, he
said again, but "nothing else than certain properties of light which, now
discovered, I think are not difficult to prove, and which if I did not know to
be true, I should prefer to reject as vain and empty speculation, than
acknowledge them as my hypothesis." Oldenburg suggested that he respond
without mentioning names ‑ especially Hooke's ‑ but Newton had a
different idea. Months went by, and his rancor festered. When he finally penned
a long reply, it named Hooke in its first sentence and on every page. "I
was a little troubled to find a person so much concerned for an Hypothesis," he wrote, "from
whome in particular I most expected an unconcerned & indifferent
examination."
Mr Hook thinks himselfe Concerned to reprehend me.... But he knows well
that it is not for one man to prescribe rules to the studies of another,
especially not without understanding the grounds on which he proceeds. Had he
obliged me with a private letter.
Hooke's rejection
of the experimentum crucis was
"a bare denyall without assigning a reason," he asserted. Newton
wrote and rewrote this letter four times. It grew far longer than his original
report. He considered colors in bubbles and froth; jabbed slyly at Hooke with
suggestions for microscopy; and refined his distinction between pure colors and
compounded whiteness. There were many ways to mix colors, he suggested, to
produce white or (not so perfect and intense) gray. "The same may be
effected by painting a Top (such as Boys play with) of divers colours, for when
it is made to circulate by whipping it will appear of such a dirty color."
Above all, he
wished to assert that optics was a mathematical science, rigorous and certain;
that it depended on physical principles and mathematical proof; and that since
he had learned these principles he had met with constant success.
He implied again
and again that Hooke was not really performing the experiments. Hooke had
"maimed" his argument. Hooke insisted on "denying some things
the truth of which would have appeared by an experimentall examination."
True‑Newton conceded‑he was arguing for the corporeity of light,
but that followed from his theory, not the other way around. It was not a
fundamental supposition. In suggesting that light was composed of particles, he
had carefully used the word perhaps.
"I wonder how Mr Hook could imagin that when I had asserted the Theory
with the greatest rigor, I should be so forgetfull as afterwards to assert the
fundamentall supposition it selfe with no more than a perhaps. "
Hooke was Newton's
most enthusiastic antagonist now, but not his most able. Christiaan Huygens,
the great Dutch mathematician and astronomer, also favored a wave theory of
light. His understanding of refraction and reflection was profound‑and
correct enough, when alloyed with Newton's, to survive up to the quantum era.
But he, too, by way of letters to Oldenburg, raised initial questions about
Newton's "hypothesis" and in return felt the young man's wrath. He
caught subtle errors that Newton would never quite acknowledge; for example,
Huygens suggested correctly that white could be created not just by a mixture
of all colors but by the blending of pairs such as blue and yellow. Fifteen months after his election to the
Royal Society, Newton announced that he wished to withdraw ‑ and not just
from the society but from all correspondence. "I suppose there hath been
done me no unkindness," he wrote Collins. "But I could wish I had met
with no rudeness in some other things. And therefore I hope you will not think
it strange if to prevent accidents of that nature for the future I decline that
conversation which hath occasioned what is past."
Oldenburg begged
him to reconsider, suggested he no longer feel obliged to pay his dues, and
assured him that the Royal Society esteemed and loved him. The criticism had
been so mild and so ordinary, though perhaps there had been
"incongruities." Newton had still never met any of these men ‑
Oldenburg, Collins, Hooke, or the others. He wrote one more reply. "The
incongruities you speak of, I pass by," he said. "But ... I intend to
be no further sollicitous about matters of Philosophy. And therefore I hope you
will not take it ill if you find me ever refusing doing any thing more in that
kind." Oldenburg, did not hear from him again for more than two years.
He had discovered a
great truth of nature. He had proved it and been disputed. He had tried to show
how science is grounded in concrete practice rather than grand theories. In
chasing a shadow, he felt, he had sacrificed his tranquillity.
Chapter
8 In the Midst of a Whirlwind
When
he observed the world it was as if he had an extra sense organ for peering into
the frame or skeleton or wheels hidden beneath the surface of things. He sensed
the understructure. His sight was enhanced, that is, by the geometry and
calculus he had internalized. He made associations between seemingly disparate
physical phenomena and across vast differences in scale. When he saw a tennis
ball veer across the court at Cambridge, he also glimpsed invisible eddies in
the air and linked them to eddies he had watched as a child in the rock‑filled
stream at Woolsthorpe. When one day he observed an air‑pump at Christ's
College, creating a near vacuum in a jar of glass, he also saw what could not
be seen, an invisible negative: tthat the reflection on the inside of the glass
did not appear to change in any way. No one's eyes are that sharp. Lonely and
dissocial as his world was, it was not altogether uninhabited; he communed
night and day with forms, forces, and spirits, some real and some imagined.
In 1675 Newton
journeyed to London and finally appeared at the Royal Society. He met in person
these men who had till then been friends and antagonists twice removed, their
spirits channeled through Oldenburg's mail. Among the virtuosi made flesh was
Robert Boyle, fifteen years his senior and a mentor of Hooke's. Boyle was a
fervent corpuscularian; in his great polemic The Sceptical Chymist he had developed a theory of fundamental
particles as the constituents of matter. He believed that all the phenomena of
nature could be explained by the combination and organization of these atoms
into mixed bodies, some perfect and some imperfect and none more perfect than
gold. He believed in the alchemists'
greatest dream, the transmutation of baser metals into gold, but he reviled
their traditions of secrecy ‑ "their obscure, ambiguous, and almost
Aenigmatical Way of expressing what they pretend to Teach.”
They have no mind to be understood at all, but by the Sons of Art (as
they call them) nor to be understood even by these without Difficulty and
Hazardous Tryalls.
His experiments
with an air‑pump were renowned, and his own investigation of color had
spurred Hooke and Newton in turn. He greeted Newton warmly.
Over the next
months Newton, back in Cambridge, labored over a new manuscript. He set down in
passionate words his own corpuscular theory. Here, finally, was his Hypothesis ‑ he embraced the label
he had denied so vehemently before. "An Hypothesis," he titled it,
"explaining the Properties of Light discoursed of in my severall
Papers.” But he spoke of more than
light alone; he was taking on the whole substance of nature. His nemesis,
Hooke, loomed large. "I have observed the heads of some great virtuoso's
to run much upon Hypotheses," Newton said, "as if my discourses
wanted an Hypothesis to explain them by." He noted that "some"
could not quite take his meaning when he spoke of light and color in the
abstract, and perhaps they would understand better with an illustration. Thus‑the
"Hypothesis."
He wanted Oldenburg
to read this to the assembled Royal Society but not to publish it. And he
wanted his listeners to understand a delicate rhetorical point. He did not
pretend to mathematical certainty here, even if, for convenience, he chose to
"speak of it as if I assumed it & propounded it to be beleived."
Let no man "think me obligd to answer objections against this
script," he said. "For I desire to decline being involved in such
troublesome & insignificant Disputes."
This sheaf of
papers posted to Oldenburg5 blended calculation and faith. It was a work of the
imagination. It sought to reveal nothing less than the microstructure of
matter. For generations it reached no further than the few men who heard it
read and then raptly debated it through all the meetings of the Royal Society
from December 1675 to the next February. Newton had peered deeper into the core
of matter than could be justified by the power of microscopes. Through a series
of experiments and associations he seemed to feel nature's fundamental
particles just beyond the edge of his vision. Indeed, he predicted that
instruments magnifying three or four thousand times might bring atoms into
view.
He saw a vast range
of phenomena to explain, and the cool certainties of geometry had reached the
limit of their usefulness here. There were all kinds of chemical activity,
processes like vegetation, fluids that interacted with more or less
"sociableness." He closed his eyes to no problem because it was too
mysterious or intractable. He confounded the distant members of the society
with a vivid description of an experiment revealing electricity, a power certain bodies gained when excited: he rubbed
a glass disk with cloth and then waved it over bits of paper. They sprang to
life:
Sometimes leaping up to the Glass & resting there a while, then
leaping downe & resting there, then leaping up & perhaps downe & up
again ... sometimes in lines perpendicular to the Table, Sometimes in oblique
ones ... & turn often about very nimbly as if... in the midst of a
whirlwind.
Irregular
motions, he emphasized‑and he saw no way to explain
them mechanically, purely in terms of matter pressing on matter. It was no
static world, no orderly world he sought to understand now. Too much to explain
at once: a world in flux; a world of change and even chaos. He gave out poetry:
For nature is a perpetuall circulatory worker, generating fluids out of
solids, and solids out of fluids, fixed things out of volatile, & volatile
out of fixed, subtile out of gross, & gross out of subtile, Some things to
ascend & make the upper terrestriall juices, Rivers and the Atmosphere; and
by consequence others to descend ....
The ancients had
often supposed the existence of ether, a substance beyond the elements, purer
than air or fire. Newton offered the ether as a hypothesis now, describing it
as a "Medium much of the same constitution with the air, but far rarer,
subtiler & more strongly Elastic." As sound is a vibration of the air,
perhaps there are vibrations of the ether‑these would be swifter and
finer. He estimated the scale of sound waves at a foot or half‑foot,
vibrations of ether at less than a hundred thousandth of an inch.
This ether was a
philosophical hedge, a way of salvaging a mechanical style of explanation for
processes that seemed not altogether mechanical: iron filings near a magnet
arrange themselves into curved lines, revealing "magnetic effluvia";
chemical change occurs in metals even after they have been sealed in glass; a
pendulum swings far longer in a glass emptied of air, but ceases eventually
nonetheless, proving that "there remains in the glass something much more
subtle which damps the motion of the bob." The mechanists were laboring to
banish occult influences‑mysterious action without contact. The ether,
more subtle than air, yet still substantial, might convey forces and spirits,
vapors and exhalations and condensations. Perhaps an ethereal wind blew those
fluttering bits of paper. Perhaps the brain and nerve transmitted ethereal
spirit ‑ the soul inspiring muscle by impelling it through the
nerves. Perhaps fire and smoke and
putrefaction and animal motion stemmed from the ether's excitation and swelling
and shrinking. Perhaps this ether served as the sun's fuel; the sun might
imbibe the ethereal spirit "to conserve his Shining, & keep the
Planets from recedeing further from him."" (The apple had dropped
long since, but universal gravitation remained remote.)
Hooke, listening to
Oldenburg read Newton's words aloud, kept hearing his name. "Mr Hook, you
may remember, was speaking of an odd straying of light ... near the edge of a
Rasor. . . ." Indeed, earlier in 1675 Hooke had put forward his new
discovery of the phenomenon later known as diffraction: the bending of light at
a sharp edge. One way to explain diffraction‑the only way, until quantum
mechanics‑was in terms of the interference of waves. Did this spreading
of light rays mean that they could curve after all, as sound waves apparently
do around corners? Newton said he was unsure: "I took it to be onely a new
kind of refraction, caused perhaps by the externall a!thers beginning to grow
rarer a little before it come at the Opake body. . . . " He recalled,
though, that Hooke had been pleased to answer that though it should be but a
new kind of refraction, yet it was a new
one. What to make of this unexpected reply, I knew not, haveing no other
thoughts but that a new kind of refraction might be as noble an Invention as
any thing els about light.
A noble invention,
Newton agreed. But he remembered having read about this experiment before
Hooke's account. He was obliged to mention that the French Jesuit Honore Fabri
had described it; and Fabri in turn had got it from a Bolognese mathematician,
Francesco Maria Grimaldi. It was not
Hooke's discovery.
Hooke grew irate.
In evenings that followed he met with friends in coffee ‑ houses and told
them that Newton had commandeered his pulse theory. After all, Newton was
talking about color in terms of "vibrations of unequal bignesses."
Large vibrations are red ‑ or, as he said more carefully, cause the
sensation of red. Short vibrations produce violet. 'Me only difference between
colors was this: a slight, quantifiable divergence in the magnitude of vibration.
Newton did not speak of waves. Nor for that matter had Hooke: waves were still
a phenomenon of the sea. A lack of vocabulary hindered both men; but what
Newton had seen was just what Hooke had sought.
This was
insupportable. At the end of the second meeting devoted to the Newton
"Hypothesis," Hooke rose to declare that the bulk of it had come from
his Micrographia, ,, which Mr Newton
had only carried farther in some particulars." Oldenburg lost no time in
reporting this claim back to Cambridge.
Cambridge fired
back. "As for Mr Hook's insinuation," Newton wrote Oldenburg, "I
need not be much concerned at the liberty he takes." He wished to avoid "the savour of
having done any thing unjustifiable or unhansome towards Mr Hook." So he
analyzed the chain of logic and priority. First, what is actually Hooke's? We
must "cast out what he has borrowed from Des Cartes or others":
That there is an ether. 'Mat light is the action of this ether. That
the ether penetrates solid bodies in varying degrees. That light is at first
uniform. That colors come from a modification of light rays‑accelerated
to make red and retarded to make blue, all other colors coming from some
mixture of red and blue.
All Hooke did was
change Descartes's idea of a pressing motion in the ether to a vibrating one.
Globules for Descartes, pulses for Hooke. "In all this," Newton
concluded,
I have nothing common with him but the
supposition that sether is a Medium susceptible of vibrations of which
supposition I make a very different use: he supposing it light it self which I
suppose it not.
For the rest‑refraction
and reflection and the production of colors‑Newton said he explained it
all so differently from Hooke as to "destroy all he has said." He
added sarcastically, "I suppose he will allow me to make use of what I
tooke the pains to find out."
Hooke was poking at
a soft spot in Newton's understanding of light. Was it particle or wave? Newton
was vacillating on this matter now, as humanity would continue to vacillate
until twentieth‑century physicists vanquished the paradox by accepting
it. Newton both exposed his uncertainty and concealed it. He played a delicate
game, ringing changes on the word hypothesis,
trying, to distinguish between what he knew and what he was forced to
suppose. He supposed the existence of an ether‑mysterious and even
spiritual because he could not dispense with such a thing, for now.
Oldenburg ‑‑
no friend to Hooke ‑ chose to surprise him with a public reading of
Newton's rejoinder at the next Royal Society meeting. Finally, after years of
jousting by proxy, Hooke decided to take pen in hand and address his adversary
personally. He adopted a meek and
philosophical tone. He said he suspected Newton was being misinformed; he had
experience with such "sinister practices." He did not wish to contend
or feud or be "drawn to such kind of warr." We are "two hard‑to‑yield
contenders," he proclaimed. "Your Designes and myne I suppose aim
both at the same thing which is the Discovery of truth and I suppose we can
both endure to hear objections."
Newton's famous
reply came a fortnight later. If the weapons of this duel were to be insincere
politesse and exaggerated deference, he could wield them as well. He called
Hooke a "true Philosophical spirit." He gladly embraced the proposal
of a private correspondence. "What's done before many witnesses is seldome
without some ftirther concern than that for truth: but what passes between
friends in private usually deserves the name of consultation rather than
contest, & so I hope it will prove between you & me." And then,
for the matter of their dispute, he
put on record a finely calibrated piece of faint praise and lofty sentiment:
What Descartes did was a good step.
You have added much several ways, & especially in taking the colours of
thin plates into philosophical consideration. If I have seen further it is by
standing on the sholders of Giants.
The private
philosophical dialogue between Newton and Hooke never took place. Almost two
years passed before they communicated again at all. By then Oldenburg had died,
Hooke had succeeded him as Secretary of the Royal Society, and Newton had
withdrawn ever more deeply into the seclusion of his Trinity chambers.
Chapter
9 All Things Are Corruptible
His
devotion to philosophical matters grew nonetheless. He built a special chimney
to carry away the smoke and fames.
By Newton's
thirties his hair was already gray, falling to his shoulders and usually
uncombed. He was thin and equine, with a strong nose and gibbous eyes. He
stayed in his chamber for days at a time, careless of meals, working by
candlelight. He was scarcely less isolated when he dined in the hall. The
fellows of Trinity College learned to leave him undisturbed at table and to
step around diagrams he scratched with his stick in the gravel of the walkways.
They saw him silent and alienated, with shoes down at heel and stockings
untied. He feared disease‑plague and pox‑and treated himself
preemptively by drinking a self‑made elixir of turpentine, rosewater,
olive oil, beeswax, and sack. In fact he was poisoning himself, slowly, by
handling mercury.
No one could
understand till centuries later‑after his papers, long hidden and
scattered, began finally to be reassembled‑that he had been not only a
secret alchemist but, in the breadth of his knowledge and his experimentation,
the peerless alchemist of Europe. Much later, when the age of reason grew
mature, a fork was seen to have divided the road to the knowledge of
substances. On one path, chemistry: a science that analyzed the elements of
matter with logic and rigor. Left behind, alchemy: a science and an art,
embracing the relation of the human to the cosmos; invoking transmutation and
fermentation and procreation. Alchemists lived in a realm of exuberant,
animated forces. In the Newtonian world of formal, institutionalized science,
it became disreputable.
But Newton belonged
to the pre‑Newtonian world. Alchemy was in its heyday. A squalid flavor
did attach to such researches; alchemists were suspected as charlatans
pretending to know how to make gold. Yet the modern distinction between
chemistry and alchemy had not emerged. When the vicar John Gaule, an expert on
witchcraft, assailed "a kinde of praestigious, covetous, cheating
magick," he called this malodorous practice by its name: chymistry. If alchemists were known to treasure secrecy
and obscure their writings with ciphers and anagrams, these habits were no bar
for Newton, burrowing further inward. If they revered arcane authorities and
certain sacred texts, if they adopted Latinate pseudonyms and circulated secret
manuscripts, so for that matter did Christian theologians. Newton was a
mechanist and a mathematician to his core, but he could not believe in a nature
without spirit. A purely mechanical theory for the world's profusion of
elements and textures‑and for their transformations, from one substance
to another‑lay too far beyond reach.
He met with
mysterious men and copied their papers‑a WS., a Mr. F. He devised a pseudonym, Feova sanctus unus, an anagram of Isaacus
Neuutonus. In the garden outside his room he built a laboratory, a shed
abutting the wall of the chapel. His fire burned night and day. To alchemists
nature was alive with process. Matter was active, not passive; vital, not
inert. Many processes began in the fire: melting, distilling, subliming, and
calcining. Newton studied them and practiced them, in his furnaces of tin and
bricks and firestones. In sublimation vapors rose from the ashes of burned
earths and condensed again upon cooling. In calcination fire converted solids
to dust; "be you not weary of calcination," the alchemical fathers
had advised; "calcination is the treasure of a thing.” When a crimson‑tinged
earth, cinnabar, passed through the fire, a coveted substance emerged:
"silvery water" or "chaotic water"‑ quicksilver. It was a liquid and a metal at once,
lustrous white, eager to form globules. Some thought a wheel rimmed with
quicksilver could turn unaided‑perpetual motion. Alchemists knew
quicksilver as Mercury (as iron was Mars, copper Venus, and gold the sun); in
their clandestine writings they employed the planet's ancient symbol, Or they
alluded to quicksilver as "the serpents."
"The two
serpents ferment well . . Newton wrote at one session. "When the
fermentation was over I added 0 16gr & the matter swelled much with a
vehement fermentation. . . . "M Like other alchemists, he conceived of
mercury not Just as an element but as a state or principle inherent in every
metal. He spoke of the "mercury" of gold. He particularly coveted a
special, noble, "philosophical" mercury: "this 0 ... drawn out
of bodies hath as many cold superfluities as common 0 hath, & also a
special form & qualities of the metals ftom which it was extracted. Part of
mercury's esoteric appeal was its tendency to react with other metals. Applied
to copper, lead, silver, and even gold, it formed soft amalgams. A skillful
practitioner could use mercury to purify metals. Over time, mercury builds up
in the body, causing neurological damage: tremors, sleeplessness, and sometimes
paranoid delusions.
Robert Boyle, too,
was experimenting with mercury. In the spring of 1676, Newton read in the Philosophical Transactions an account
"Of the Incalescence of Quicksilver with Gold, generously imparted by
B.R." He recognized the inverted initials,
and he suspected that the research drew near the alchemists' dream of
multiplying gold. "I believe the fingers of many will itch to be at the
knowledge of the preparation of such a 0," he wrote privately. A dangerous
sort of knowledge might lie nearby‑"an inlet to something more
noble, not to be communicated without immense damage to the world." Newton believed‑and knew Boyle did,
too‑that the basic substance of matter was everywhere the same; that
countless shapes and forms flowed from the varied operations of nature on this
universal stuff. Why should the transmutation of metals be impossible then) The
history of change was all around.
Like no other experimenter of his time,
alchemist or chemist, he weighed his chemicals precisely, in a balance scale. Obsessed as always with the finest degrees
of measurement, he recorded weights to the nearest quarter of a grain. He
measured time, too; here, a precise unit was an eighth of an hour. But
measurement never replaced sensation: as his experiments fumed, he touched and
sniffed and tasted the slimes and liquors that emerged.
He
probed for the processes of life and death: vegetation and, a special case,
putrefaction, which produces a "blackish rotten fat substance" and
exhales matter into ftimes. Nothing can
be changed from what it is without putrefaction, he wrote in haste, in his
microscopic scrawl. First nature putrefies, then it generates new things. All things are corruptible. All things are generable. And so the world
continually dies and is reborn. 'Mese exhalations, and mineral spirits, and
watery vapors, generate a rising air and buoy up the clouds: "so high as
to loos their gravity."
This
is very agreeable to natures proceedings to make a circulation of all things.
'Mus this Earth resembles a great animall or rather inanimate vegetable, draws
in aethereall breath for its dayly refreshment and vital ferment.... This is
the subtil spirit which searches the most hiden recesses of all grosser matter
which enters their smallest pores and divides them more subtly then any other
materiall power what ever.
Driving
this cycle of death and life, inspiring this circulatory world, must be some
active spirit‑nature's universal agent, her secret fire. Newton could not
but identify this spirit with light itself‑and light, in turn, with God.
He marshaled reasons. All things, in the fire, can be made to give off light.
Light and heat share a mutual dependence. No substance so subtly pervades all
things as light. He felt this in the depth of his being.
"Noe heat is
so pleasant & beamish as the suns," he wrote.
Through his
alchemical study shines a vision of nature as life, not machine. Sexuality
suffused the language of alchemy. Generation came from seed and copulation;
principles were male (Mercury) and female (Venus). Then again:
these two mercuries are the masculine and feminine semens ... fixed and
volatile, the Serpents around the Caduceus, the Dragons of Flammel. Nothing is
produced from masculine or feminine semen alone.. . . The two must be joined.
From
the seeds, the seminal virtues, came the fire and the soul. If alchemy was the
closest Newton came to a worldly exploration of sexuality, it crossed paths
with a theological quest as well. To alchemists the transmutation of metals
meant a spiritual purification. It was God who breathed life into matter and
inspired its many textures and processes. Tbeology joined alchemy as the chief
preoccupation of Newton's middle decades.
The new mechanical
philosophers, striving to create a science free of occult qualities, believed
in matter without magic‑inanimate brute matter, as Newton often called
it. The virtuosi of the Royal Society wished to remove themselves from
charlatans, to build all explanations from reason and not miracles. But magic
persisted. Astronomers still doubled as astrologers; Kepler and Galileo had
trafficked in horoscopes. The magician,
probing nature's secrets, served as a template for the scientist. "Do you
believe then," Nietzsche asked two centuries later, "that the
sciences would ever have arisen and become great if there had not beforehand
been magicians, alchemists, astrologers and wizards, who thirsted and hungered
after abscondite and forbidden powers?"
Descartes
had gone to great lengths to purify his scheme, substituting mechanical (but
imaginary) vortices for hidden (but real) forces like magnetism. Newton was
rebelling against Descartes, and nowhere more fiercely than in the realm of the
very small. The philosophers stood further removed from atoms than from the
stars. Atoms remained a fancy, invisible to human sight. The forces governing
heavenly bodies were invisible too, but ready to be inferred from a
mathematical treatment of the accumulating data. For any practitioner of
chemistry or alchemy, one question loomed: what made particles cohere in the
first place? What caused inert atoms to stick together, to form minerals and
crystals and‑even more wonderfully‑plants and animals? The
Cartesian style was recklessly ad hoc, Newton thought. It offered a different
mechanical explanation for every new phenomenon: one for air, another for
water, another for vinegar, yet another for sea salt‑"and so of
other things: your Philosophy will be nothing else than a system of
Hypotheses.” Newton wanted a universal cause.
As with the
question of light's true nature, he chose a narrow rhetorical path: veering
past the question of whether his program was or was not fundamentally
mechanical, all reduced to particles and forces. Of light he had said,
"Others may suppose it multitudes of unimaginable small & swift
Corpuscles of various sizes, springing from shining bodies at great distances,
one after another, but yet without any sensible interval of time, &
continually urged forward by a Principle of motion.” For the rest:
God who gave Animals self motion beyond our understanding is without
doubt able to implant other principles of motion in bodies which we may
understand as little. Some would readily grant this may be a Spiritual one; yet
a mechanical one might be showne....
Rather than turn away from what he could not explain, he plunged in
more deeply. Dry powders refused to cohere. Flies walked on water. Heat
radiated through a vacuum. Metallic particles impregnated mercury. Mere thought
caused muscles to contract and dilate. There were forces in nature that he
would not be able to understand mechanically, in terms of colliding billiard
balls or swirling vortices. They were vital, vegetable, sexual forces‑invisible
forces of spirit and attraction. Later, it had been Newton, more than any other
philosopher, who effectively purged science of the need to resort to such
mystical qualities. For now, he needed them.
When he was not
stoking his furnaces and stirring his crucibles, he was scrutinizing his
growing hoard of alchemical literature. By the century's end, he had created a
private Index chemicus, a manuscript
of more than a hundred pages, comprising more than five thousand individual
references to writings on alchemy spanning centuries. This, along with his own
alchemical writing, remained hidden long after his death.
Chapter
10 Heresy, Blasphemy, ldollatrv
The
fatherless man, the fellow of the college named Trinity, turned to Christian
theology with the same sleepless fervor he brought to alchemy. He started a
notebook, writing Latin headings atop the folios: Life of Christ; Miracles of
Christ; Passion, Descent, and Resurrection. Some topics remained forever blank;
some filled and then overflowed with intense, scholarly, and troubled notes.
The topics that most absorbed his interest were the relation of God and Christ,
the father and the son, and most of all, De
Trinitate, Of the Trinity.' Here he swerved into heresy. He abjured this
central dogma of his religion: three persons in one Godhead, holy and
undivided. He denied the divinity of Jesus and of the Holy Ghost.
England's
universities were above all else instruments of Christianity, and at each step
in his Cambridge career Newton swore oaths avowing his faith. But in the
seventh year of his fellowship, 1675, a further step would be required: he would
take holy orders and be ordained to the Anglican clergy, or he would face
expulsion. As the time approached, he realized that he could no longer affirm
his orthodoxy. He would not be able to take a false oath. He prepared to
resign.
He
believed in God, not as a matter of obligation but in the warp and weft of his
understanding of nature. He believed in God eternal and infinite; a living and
powerful Lord holding sway over all things; omnipresent, in bodies and filling the space that is empty of body. He
believed in God as immovable‑and this belief fused with his vision, still
not quite defined, of absolute space. Newton's God had established the rules by
which the universe operates, a handiwork that humans must strive to know. But
this God did not set his clockwork in motion and abandon it.
He
is omnipresent not only virtually but
also substantially.... In him all
things are contained and move, but he does not act on them nor they on him....
He is always and everywhere.... He is all eye, all ear, all brain, all arm, all
force of sensing, of understanding, and of acting.
If
God was immutable, religion was not. Close study fed both his faith and his
heresy. He researched and wrote the history of the church again and again. He
read the Scriptures literally and indulged a particular fascination with
prophecy, which he saw as complex symbolism to be unraveled and interpreted. He
considered this a duty. He set down a catalogue of fifteen rules of
interpretation and seventy figures of prophecy. He sought the facts, dates, and
numbers. He calculated and then recalculated the time of the Second Coming,
which he understood to be the restoration of primitive uncorrupted
Christianity. He studied in detail the description of the Temple of Jerusalem,
a structure of "utmost simplicity and harmony of all its
proportions,” and tried to reconstruct
its floor plan from the long, rambling algorithms of the Hebrew Book of Ezekiel‑
So
he measured the length thereof, twenty cubits; and the breadth, twenty cubits,
before the temple: and he said unto me, This is the most holy place. After he
measured the wall of the house, six cubits; and the breadth of every side
chamber, four cubits, round about the house on every side. And the side
chambers were three, one over another, and thirty in order....
‑an intricate
puzzle in prose, another riddle to be deciphered. He struggled to work out the
length of the ancient cubit. There seemed to be a message meant for him.
And
if they be ashamed of all that they have done, shew them the form of the house,
. . and all the forms thereof, and all the ordinances thereof, and all the
forms thereof, and all the laws thereof. and write it in their sight.
The very existence
of the Bible in English‑long opposed by the church establishment and
finally authorized only a generation before Newton's birth‑had inspired
the Puritan cause. Vernacular versions of the Bible encouraged the laity to
look into the texts and make their own interpretations. Scholars applied the
new philosophical tools to Scripture. Anyone could pursue biblical inquiry as a
self‑directed enterprise; many tried to distinguish the pure Gospel from
its medieval accretions. Ancient controversies came back to life. Newton was
studying no less than the history of worship. He compared the Scriptures in the
new English translation and in the ancient languages; he collected Bibles in
Latin, Greek, Hebrew, and French. He sought out and mastered the writings of
the early fathers of the church: saints and martyrs, Athanasius and Arius,
Origen, author of the Hexapla, Eusebius
of Caesarea and Epiphanius of Constantia, and dozens more. He embroiled himself
in the great controversy that tore at Christendom through the fourth century,
at Nicaea and Constantinople.
The Trinity was a
mystery. It defied rational explanation. It rested on a paradox that could be
neither comprehended nor demonstrated: that the Son is fully human and fully
divine. As a human Christ does not understand his divinity all at once.
Nonetheless he is of the same being, homoousious, as the Father. One God:
Father, Son, and Holy Spirit.
In the early fourth
century, Arius, an ascetic churchman in Alexandria, led a rebellion against
this doctrine. He taught that God alone is fully divine and immutable; that the
Son was created, subordinate, and subject to growth and change. For this heresy
Arius was excommunicated and condemned. His writings were burned. But enough
survived to persuade Newton, brooding over them a millennium later, that the
Trinitarians had carried out a fraud upon Christianity. The fraud had been
perfected by monks and popes. The word trinity never appears in the New
Testament. For explicit foundation in Scriptures, the orthodox looked to the
First Epistle of John: "For there are three that bear record in heaven,
the Father, the Word, and the Holy Ghost: and these three are one." Only
the King James Version had the last phrase. Newton's critical reading persuaded
him that the original texts had been deliberately debased in support of false
doctrine‑a false infernal religion.
In theology as in
alchemy, he felt himself to be questing for ancient truths that had been
perverted in the dark history of the past centuries. Knowledge had been lost,
veiled in secret codes to hide it from the vulgar, distorted by blasphemers,
priests and kings. He believed this to be true of mathematics, too, the
language of God. In all these realms, he tried to recover words and laws once
known and then lost. He had a mission. He believed he was doing God's work.
"Just as the world was created from dark Chaos through the bringing forth
of the light," he wrote in one manuscript, ". . . so our work brings
forth the beginning out of black chaos and its first matter." In both
alchemy and theology, he cherished secrecy just as the new philosophers in
London repudiated it. No public science here: rather, meetings with anonymous
confidantes, barter of manuscripts, shadowy brotherhoods.
Arianism was
undergoing a clandestine revival, but disbelief in the holy Trinity amounted to
dangerous heresy nonetheless. By putting his arguments to paper Newton
committed a crime that, if exposed, could have cost him his position and even
his freedom."
At the last moment,
in 1675, Newton's precarious position at Cambridge was rescued. The king
granted his request for a dispensation, an act that released the Lucasian
professorship, in perpetuity from the obligation to take holy orders. This did not end his theological obsession.
He perfected his heresy through decades of his life and millions of words. He
marshaled his arguments and numbered them:
1.
The [word] God is no where in the scriptures used to signify more then one of
the thre persons at once.
2.
The word God put absolutely without particular restriction to the Son or Holy
ghost doth always signify the Father from one end of the scriptures to the
other....
6. The son confesseth the father greater then
him calls him his God, &c....
11.
The son in all things submits his will to the will of the father. which could
be unreasonable if he were equall to the father.
No
gulf divided Newton's theological reasoning from his physics and geometry.
Logic proved that any divinity in the subordinate aspects of God remained
derived from and dependent upon God. He drew a diagram:
To
make this plainer suppose a, b &
c are 3 bodies of which a hath gravity originally in it self by which it
presseth upon b & c which are
without any originall gravity a but
yet by the pressure of a communicated to them do presse downwards as much as A
doth. Then there would be force in a, force in b & force in c, & yet they are not thre forces but one
force which is originally in a & by communication/descent in
b
& c.
He would not even
label years as AD, preferring Ac: Christ, but not the Lord. Jesus was more than
a man but less than God. He was God's son, a mediator between God and humanity,
chosen to be a prophet and messenger, and exalted to God's right hand. If we
could decipher the prophecies and the messages, we would know a God of order,
not chaos; of laws, not confusion. Newton plumbed both nature and history to
find out God's plan. He rarely attended church.
Anger blazed
through his theology; reason followed along behind. In his reading notes and
"articles" and "points" and "observations," his
"Short Schem of the True Religion" and his analysis of prophecies and
revelations, he raged against the blasphemers. He called them fornicators ‑
for he associated this special blasphemy with lust. “Seducers waxing worse and
worse," he wrote, "deceiving and being deceived ‑ such as will
not endure sound doctrine but after their own lusts heap to themselves
teachers, having itching ears and turning away their ears from the truth."
Monks, with their unclean thoughts, had perpetrated this corruption.
He felt
Trinitarianism. not just as error but as sin, and the sin was idolatry. For
Newton this was the most detested of crimes. It meant serving false gods ‑
"that is, Ghosts or Spirits of dead men or such like beings." Kings
were specially prone to it, "kings being apt to enjoyn the honour of their
dead ancestors," declared this obsessive scholar, who, for himself, could
not have been less apt to call on the honor of dead ancestors.
He had seldom
returned home to Lincolnshire since the sojourn of the plague years, but in the
spring of 1679 his mother succumbed to a fever. He left Cambridge and kept
vigil with her over days and nights, till she died. He, the first‑born
son, not his half‑brother or sisters, was her heir and executor, and he
buried her in the Colsterworth churchyard next to the grave of his father.
Chapter
11 First Principles
In
the next year a comet came. In England it arose faint in the early morning sky
for a few weeks in November till it approached the sun and faded in the dawn.
Few saw it.
A more dramatic
spectacle appeared in the nights of December. Newton saw it with naked eye on
December 12: a comet whose great tail, broader than the moon, stretched over
the full length of King's College Chapel. He tracked it almost nightly through
the first months of 1681. A young
astronomer traveling to France, Edmond Halley, a new Fellow of the Royal
Society, was amazed at its brilliance.
Robert Hooke
observed it several times in London. Across the Atlantic Ocean, where a handful
of colonists were struggling to survive on a newfound continent, Increase Mather
delivered a sermon, "Heaven's Alarm to the World," to warn Puritans
of God's displeasure.
Halley served as a
sometime assistant to a new officeholder, the Astronomer Royal. This was John
Flarnsteed, a clergyman and self‑taught skywatcher appointed by the King
in 1675, responsible for creating and equipping an observatory on a hilltop
across the River Thames at Greenwich. The Astronomer's chief mission was to
perfect star charts for the Navy's navigators. Flamsteed did this assiduously,
recording star places with his telescope and sextant night after night, more
than a thousand observations each year. Yet he had not seen the November comet.
Now letters from England and Europe alerted him to it.
Whatever comets
were, omens or freaks, their singularity was taken for granted: each glowing
visitor arrived, crossed the sky in a straight path, and departed, never to be
seen again. Kepler had said this authoritatively, and what else could a culture
of short collective memory believe?
But this year
European astronomers recorded two: a faint predawn comet that came and went in
November 1680, and a great giant that appeared a month later and dominated the
skies till March. Flamsteed thought comets might behave like planets. Immersed as he was in the geometry of the
sky, charting the changes in celestial perspective as the earth orbited the
sun, he predicted that the comet he had missed in November might yet return. He
watched the sky for it. His intuition was rewarded; he spied a tail on December
10, and the tail and head together, near Mercury, two days later. He had a
friend at Cambridge, James Crompton, and he sent notes of his observations,
hoping Crompton could pass them on to Newton. A fortnight later he wrote again,
speculating, "If we suppose it a consumeing substant 'tis much decayed and
the Fuell spent which nourishes the blaze but I have much to say against this
hypothesis however you may consider of it and Pray let me have your
opinion.” Newton read this and remained
silent.
A month later
Flamsteed tried again. "It may seem that the exteriour coat of the Comet
may be composed of a liquid.... It was never well defined nor shewed any
perfect limb but like a wisp of hay.”
He was persuaded more than ever that the two comets were one. After all,
he had predicted the reappearance. He struggled to explain the peculiar motion
he had recorded. Suppose, he said, the sun attracts the planets and other
bodies that come within its "Vortex" ‑ perhaps by some form of
magnetism. Then the comet would approach the sun in a straight line, and this
path could be bent into a curve by the pressure of the ethereal vortex. How to
explain its return? Flamsteed suggested a corresponding force of repulsion; he
likened the sun to a magnet with two poles, one attracting and one repelling.
Finally Newton
replied. He objected to the notion of magnetism in the sun for a simple reason:
"because the *** is a vehemently hot body & magnetick bodies when made
red hot lose their virtue." He was not persuaded that the two comets were one
and the same, because his exquisitely careful measurements of their transit,
and all the others he could collect ‑ 6 degrees a day, 36 minutes a day,
3 ½ degrees a day‑seemed to show
acceleration suddenly alternating with retardation. "It is very
irregular." Even so, he diagrammed Flamsteed's proposal, the comet nearing
the sun, swerving just short of it, and veering away. This he declared
unlikely. Instead he suggested that the comet could have gone all the way
around the sun and then returned. He diagrammed this alternative, too. And he
conceded a crucial point to Flamsteed's intuition: "I can easily allow an
attractive power in the *** whereby the
Planets are kept in their courses about him from going away in tangent
lines."
He had never before
said this so plainly. In the gestation of the calculus, in 1666, he had relied
on tangents to curves‑the straight lines from which curves veer, through
the accumulation of infinitesimal changes. In laying the groundwork for laws of
motion, he had relied on the tendency of all bodies to continue in straight
lines. But he had also persisted in thinking of planetary orbits as a matter of
balance between two forces: one pulling inward and the other,
"centrifugal," flinging outward. Now he spoke of just one force,
pulling a planet away from what would otherwise be a straight trajectory.
This
very conception had arrived at his desk not long before in a letter from his
old antagonist Hooke. Now Secretary to the Royal Society, in charge of the Philosophical Transactions, Hooke wrote
imploring Newton to return to the fold. He made glancing mention of their
previous misunderstandings: "Difference in opinion if such there be me
thinks shoud not be the occasion of Emnity." And he asked for a particular favor: would Newton share any
objections he might have to his idea, published five years before, that the
motions of planets could be simply a compound of a straight‑line tangent
and "an attractive motion towards the centrall body." A straight line
plus a continuous deflection equals an orbit.
Newton, just back
in Cambridge after settling his mother's affairs, lost no time in composing his
reply. He emphasized how remote he was from philosophical matters:
heartily sorry I am that I am at present unfurnished with matter
answerable to your expectations. For I have been this last half year in
Lincolnshire cumbred with concerns. . . . I have had no time to entertein
Philosophical meditations. . And before that, I had for some years past been
endeavouring to bend my self from Philosophy ... which makes me almost wholy
unacquainted with what Philosophers at London or abroad have lately been employed
about. . I am almost as little concerned about it as one tradesman uses to be
about another man's trade or a country man about learning.
Hooke's
essay offered a "System of the World." It paralleled much of Newton's
undisclosed thinking about gravity and orbits in 1666, though Hooke's system
lacked a mathematical foundation. All celestial bodies, Hooke supposed, have
"an attraction or gravitating power towards their own centers." They
attract their own substance and also other bodies that come "within the
sphere of their activity." All bodies travel in a straight line until
their course is deflected, perhaps into a circle or an ellipse, by "some
other effectual powers." And the power of this attraction depends on
distance.
Newton professed to
know nothing of Hooke's idea. "Perhaps you will incline the more to
beleive me when I tell you that I did not before the receipt of your last
letter, so much as heare (that I remember) of your Hypotheses." He threw
Hooke a sop, however: an outline of an experiment to demonstrate the earth's
daily spin by dropping a ball from a height. "The vulgar" believed
that, as the earth turns eastward under the ball, the ball would land slightly
to the west of its starting point, having been left behind during its fall. On
the contrary, Newton proposed that the ball should land to the east. At its
initial height, it would be rotating eastward with a slightly greater velocity
than objects down on the surface; thus it should "outrun" the
perpendicular and "shoot forward to the east side." For a trial, he
suggested a pistol bullet on a silk line, outdoors on a very calm day, or in a
high church, with its windows well stopped to block the wind.
He drew a diagram
to illustrate the point. In it he allowed his imaginary ball to continue in a
spiral to the center of the earth. This was an error, and Hooke pounced. Having
promised days earlier to keep their correspondence private, he now read
Newton's letter aloud to the Royal Society and publicly contradicted it.16 An
object falling through the earth would act like an orbiting planet, he said. It
would not descend in a spiral‑"nothing att all akin to a spirall"‑but
rather, "my theory of circular motion makes me suppose," continue to
fall and rise in a sort of orbit, perhaps an ellipse or "Elleptueid."
How a body falls to the center of the earth:
Newton and Hooke's debate of 1679.
a.
Newton: A body dropped ftom a height at A should be carried forward by its
motion and land to the east of the perpendicular, "quite contrary to the
opinion of the vulgar." (But he continues the path‑erroneously‑in
a spiral to the center.)
b.
Hooke: "But as to the curve Line which you seem to suppose it to Desend by
... Vizt a kind of spirall ... my theory of circular motion makes me suppose it
would be very differing and nothing att all akin to a spi . rall but rather a
kind Elleptueid."
c.
Newton: The true path, supposing a hollow earth and no resistance, would be
even more complex‑"an alternating ascent & descent."
Once again Hooke had managed to
drive Newton into a rage. Newton replied once more and retreated to silence.
Yet in their brief exchange the two men engaged as never before on the turf of
this peculiar, un‑physical, ill‑defined thought experiment. It was
"a Speculation of noe Use yet," Hooke agreed. After all, the earth
was solid, not void. They exchanged dueling diagrams.
They goaded each
other into defining the terms of a profound problem. Hooke drew an
ellipse. Newton replied with a diagram
based on the supposition that the attractive force would remain constant but
also considered the case where gravity was ‑ to an unspecified degree ‑
greater nearer the center. He also let Hooke know that he was bringing potent
mathematics to bear: "The innumerable & infinitly little motions (for
I here consider motion according to the method of indivisibles) . . ."
Both men were thinking in terms of a celestial attractive force, binding
planets to the sun and moons to the planets. They were writing about gravity as
though they believed in it. Both now considered it as a force that pulls heavy
objects down to the earth. But what could be said about the power of this
force? First Hooke had said that it depended on a body's distance from the
center of the earth. He had been trying in vain to measure this, with brass
wires and weights atop St. Paul's steeple and Westminster Abbey. Meanwhile the
intrepid Halley, an eager seagoing traveler, had carried a pendulum up a 2,500foot
hill on St. Helena, south of the equator, and judged that it swung more slowly
there.
Hooke and Newton
had both jettisoned the Cartesian notion of vortices. They were explaining the
planet's motion with no resort to ethereal pressure (or, for that matter,
resistance). They had both come to believe in a body's inherent force‑its
tendency to remain at rest or in motion a concept for which they had no name.
They were dancing around a pair of questions, one the mirror of the other:
What curve will be
traced by a body orbiting another in an inverse‑square gravitational
field? (An ellipse.)
What gravitational
force law can be inferred from a body orbiting another in a perfect ellipse?
(An inverse‑square law.)
Hooke finally did
put this to Newton: "My supposition is that the Attraction always is in a
duplicate proportion to the Distance from the Center Reciprocall" ‑
that is, inversely as the square of distance. He got no reply. He tried again:
It
now remaines to know the proprietys of a curve Line ...made by a centrall
attractive power ... in a Duplicate proportion to the Distances reciprocally
taken. I doubt not but that by your excellent method you will easily find out
what that Curve must be, and its proprietys, and suggest a physicall. Reason of
this proportion.
Hooke
had finally formulated the problem exactly. He acknowledged Newton's superior
powers. He set forth a procedure: find the mathematical curve, suggest a
physical reason. But he never received a reply.
Four
years later Edmond Halley made a pilgrimage to Cambridge. Halley had been
discussing planetary motion in coffee‑houses with Hooke and the architect
Christopher Wren. Some boasting ensued. Halley himself had worked out (as
Newton had in 1666) a connection between an inverse‑square law and
Kepler's rule of periods‑that the cube of a planet's distance from the
sun varies as the square of its orbital year. Wren claimed that he himself had
guessed at the inverse‑square law years before Hooke, but could not quite
work out the mathematics. Hooke asserted that he could show how to base all
celestial motion on the inverse-square law and that he was keeping the details
secret for now, until more people had tried and failed; only then would they
appreciate his work. Halley doubted
that Hooke knew as much as he claimed.
Halley put the
question to Newton directly in August 1684: supposing an inverse‑square
law of attraction toward the sun, what sort of curve would a planet make?
Newton told him: an ellipse. He said he had calculated this long before. He
would not give Halley the proof ‑ he said he could not lay his hands on
it ‑ but promised to redo it and send it along.
Months passed. He
began with definitions. He wrote only in Latin now, the words less sullied by
everyday use. Quantitas materice ‑ quantity of matter. What did this mean
exactly? He tried: "that which arises from its density and bulk
conjointly." Twice the density and twice the space would mean four times
the amount of matter. Like weight, but weight
would not do; he could see ahead to traps of circular reasoning. Weight
would depend on gravity, and gravity could not be presupposed. So, quantity of matter: "This quantity
I designate under the name of body or mass.”
Then, quantity of motion: the
product of velocity and mass. And force‑innate, or impressed, or
"centripetal" ‑ a coinage, to mean action toward a center.
Centripetal force could be absolute, accelerative, or motive. For the reasoning
to come, he needed a foundation of words that did not exist in any language.
He could not, or
would not, give Halley a simple answer. First he sent a treatise of nine pages,
"On the Motion of Bodies in Orbit.”
It firmly tied a centripetal force, inversely proportional to the square
of distance, not only to the specific geometry of the ellipse but to all
Kepler's observations of orbital motion. Halley rushed back to Cambridge. His
one copy had become an object of desire in London. Flamsteed complained:
"I beleive I shall not get a sight of Lit] till our common freind Mr Hooke
& the rest of the towne have been first satisfied.” Halley begged to publish the treatise, and
he begged for more pages, but Newton was not finished.
The
birth of universal gravitation: Newton proves by geometry that if a body Q
orbits in an ellipse, the implied force toward the focus S (not the center Q
varies inversely with the square of distance.
As he wrote, computed, and wrote more, he saw the pins of a cosmic lock
tumbling into place, one by one. He pondered comets again: if they obeyed the
same laws as planets, they must be an extreme case, with vastly elongated
orbits. He wrote Flamsteed asking for more data. He first asked about two
particular stars, but Flamsteed guessed immediately that his quarry was the
comet. "Now I am upon this subject," Newton said, "I would
gladly know the bottom of it before I publish my papers." He needed
numbers for the moons of Jupiter, too. Even stranger: he wanted tables of the
tides. If celestial laws were to be established, all the phenomena must obey
them,
The
alchemical furnaces went cold; the theological manuscripts were shelved. A
fever possessed him, like none since the plague years. He ate mainly in his
room, a few bites standing up. He wrote standing at his desk. When he did venture
outside, he would seem lost, walk erratically, turn and stop for no apparent
reason, and disappear inside once again. Thousands of sheets of manuscript lay
all around, here and at Woolsthorpe, ink fading on parchment, the jots and
scribbles of four decades'. undated and disorganized. He had never written like
this: with a great purpose, and meaning his words to be read.
Though he had
dropped alchemy for now, Newton had learned from it. He embraced invisible
forces. He knew he was going to have to allow planets to influence one another
from a distance. He was writing the principles of philosophy. But not just
that: the mathematical principles of natural philosophy. "For the whole
difficulty of philosophy," he wrote, Ccseems to be to discover the forces
of nature from the phenomena of motions and then to demonstrate the other
phenomena from these forces." The planets, the comets, the moon, and the
sea. He promised a mechanical program – no occult qualities. He promised proof. Yet there was mystery in his forces still.
First
principles. ,Time, space, place, and motion" ‑ he wished to blot out
everyday knowledge of these words. He gave them new meanings, or, as he saw it,
redeemed their true and sacred meanings. He had no authority to rely on‑this
unsocial, unpublished professor‑so it was a sort of bluff, but he made
good on it. He established time as independent of our sensations; he
established space as independent of matter. Thenceforth time and space were
special words, specially understood and owned by the virtuosi – the scientists.
Absolute, true, and mathematical time3 in
and of itself, and of its own nature, without reference to anything external,
flows uniformly...
Absolute
space, of its own true nature without reference to anything external, always
remains homogeneous and immovable . . . .
Our
eyes perceive only relative motion: a sailor's progress along his ship, or the
ship's progress on the earth. But the earth, too, moves, in reference to space ‑
itself immovable because it is purely mathematical, abstracted from our senses.
Of time and space he made a frame for the universe and a credo for a new age.
Chapter
12 Every Body Perseveres
It
was ordered, that a letter of thanks be written to Mr. NEWTON." recorded
Halley, as clerk of the Royal Society, on April 28, 1686, and that in the
meantime the book be put into the hands of Mr HALLEY."
Only Halley knew
what was in "the book" ‑ a first sheaf of manuscript pages,
copied in Cambridge by Newton's amanuensis and dispatched to London with the
grand title Philosophice Naturalis
Pncipia Mathematica. Halley had been forewarning the Royal Society: "a
mathematical demonstration of the Copernican hypothesis"; "makes out
all the phenomena of the celestial motions by the only supposition of a
gravitation towards the centre of the sun decreasing as the squares of the
distances there from reciprocally.” Hooke heard him.
It was Halley,
three weeks later, who undertook the letter of thanks: "Your Incomparable
treatise," etc. He had persuaded the members, none of whom could have read
the manuscript, to have it printed, in a large quarto, with woodcuts for the
diagrams. There was just one thing more he felt obliged to tell Newton:
"viz. that Mr Hook has some pretensions upon the invention of the rule of
the decrease of Gravity.... He sais you had the notion from him [and] seems to
expect you should make some mention of him, in the preface .... “
What
Newton had delivered was Book I of the Principia He had completed much of Book II, and
Book III lay not far behind. He interrupted himself to feed his fury, search
through old manuscripts, and pour forth a thunderous rant, mostly for the
benefit of Halley. He railed that Hooke was a bungler and a pretender:
This carriage towards me is very strange & undeserved, so that I
cannot forbeare in stating that point of justice to tell you further ... he
should rather have excused himself by reason of his inability. For tis plain by
his words he knew not how to go about it. Now is this not very fine?
Mathematicians that find out, settle & do all the business must content
themselves with being nothing but dry calculators & drudges & another
that does nothing but pretend & grasp at all things must carry away all the
invention....
Mr Hook has erred
in the invention he pretends to & his error is the cause of all the stirr
he makes....
He imagins he
obliged me by telling me his Theory, but I thought my self disobliged by being
upon his own mistake corrected magisterially & taught a Theory which every
body knew & I had a truer notion of it then himself. Should a man who
thinks himself knowing, & loves to shew it in correction & instructing
others, come to you when you are busy, & notwithstanding your excuse, press
discourses upon you & through his own mistakes correct you & multiply
discourses & then make this use of it, to boast that he taught you all he
spake & oblige you to acknowledge it & cry out injury & injustice
if you do not, I beleive you would think him a man of a strange unsociable
temper.
In
his drafts of Book II, Newton had mentioned the most illustrious Hooke ‑
"C1 [arissimus] Hookius” ‑ but now he struck all mention of Hooke
and threatened to give up on Book III. "Philosophy is such an
impertinently litigious Lady that a man had as good be engaged in Law suits as have to do with her. I found it so
formerly & now I no sooner come near her again but she gives me
warning.” Hooke had not been the first
to propose the inverse‑square law of attraction; anyway, for him it was a
guess. It stood in isolation, like countless other guesses at the nature of the
world. For Newton, it was embedded, linked, inevitable. Each part of Newton's
growing system reinforced the others. In its mutual dependency lay its
strength.
Needs
Editing from here on
Halley, meanwhile,
found himself entangled in the business of publishing. The Royal Society had
never actually agreed to print the book. Indeed, it had only underwritten the
publication of one book before, a lavish and disastrously unsuccessful two‑volume
History of Fishes.8 After much discussion
the council members did vote to order the 11~rincipia printed‑but by
Halley, at his own expense. They offered him leftover copies of History of Fishes in place of his
salary. No matter. The young Halley was a believer, and he embraced his
burden: the proof sheets mangled and lost, the complex abstruse woodcuts, the
clearing of errata, and above all the nourishing of his author by cajolement
and
EVERY BODY PERSEVERES
flattery. "You will do your self the honour
of perfecting scientifically what all past ages have but blindly groped
after."9 The flattery was sincere, at least.
Halley sent sixty copies of Philosophia‑ Naturalis Principia Mathematica on a wagon from London to
Cambridge in July 1687. He implored Newton to hand out twenty to university
colleagues and carry forty around to booksellers, for sale at five or six
shillings apiece.10 The book opened with a florid ode of praise to its author,
composed by Halley. When an adulatory anonymous review appeared in the Philosophical Transactions, this, too,
was by Halley. I
Without further ado, having defined his
terms, Newton announced the laws of motion.
Law
1. Ever body perseveres in its state of being at rest or y
of
moving uniformly straight
forward, except insofar as it is compelled to change its state by forces
impressed. A cannonball would fly in a straight line forever, were it not for
air resistance and the downward force of gravity. The first law stated,
without naming, the principle of inertia, Galileo's principle, refined. Two
states‑being at rest and moving uniformly‑are to be treated
as the same. If a flying cannonball embodies a force, so does the cannonball
at rest.
Law
2. A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force
is impressed. Force generates motion,
and these are quantities, to be added and multiplied according to mathematical
rules.
Law
3. To any action there is always an opposite and equal reaction; in other
words, the actions of two bodies upon each other
ISAAC NEWTON
are always equal and always opposite in
direction. If a finger presses a stone, the stone presses back against the
finger. If a horse pulls a stone, the stone pulls the horse. Actions are
interactions‑no preference of vantage point to be assigned.
...............
If the earth tugs at the moon, the moon tugs
back. 12
He presented these as axioms, to serve as the
foundation for an edifice of reasoning and proof. "Law"‑lex‑was
a strong and peculiar choice of words. 13 Bacon had spoken of laws, fundamental
and universal. It was no coincidence that Descartes, in his own book called
Principles of Philosophy, had attempted a set of three laws, regula quadam sive
leges naturce, specifically concerning motion, including a law of inertia. For
Newton, the laws formed the bedrock on which a whole system would lie.
A law is not a cause, yet it is more than a
description. A law is a rule of conduct: here, God's law, for every piece of
creation. A law is to be obeyed, by inanimate particles as well as sentient
creatures. Newton chose to speak not so much of God as of nature. "Nature
is exceedingly simple and conformable to herself. Whatever reasoning holds for
greater motions, should hold for lesser ones as well." 14
Newton formed his argument in classic Greek
geometrical style: axioms, lemmas, corollaries; Q.E.D. As the best model available for perfection in knowledge, it
gave his physical program the stamp of certainty. He proved facts about
triangles and tangents, chords and parallelograms,
I . . . . . . . . . .
and from there, by a long chain of argument,
proved facts about the moon and the tides. On his own path to these discoveries,
he had invented a new mathematics, the integral and differential calculus. Tle
calculus and the discoveries were of a piece. But he severed the connection
now. Rather
EVERY BODY PERSEVERES
than offer his readers an esoteric new
mathematics as the basis for his claims, he grounded them in orthodox geometry‑orthodox,
yet still new, because he had to incorporate infinities and infinitesimals.
Static though his diagrams looked, they depicted processes of dynamic change.
His lemmas spoke of quantities that constantly tend to equality or diminish
indefinitely; of areas that simultaneously approach and ultimately vanish; of
momentary increments and ultimate ratios and curvilinear limits. He drew lines
and triangles that looked finite but were meant to be on the point of vanishing.
He cloaked modern analysis in antique disguise.15 He tried to prepare his
readers for paradoxes.
It may be objected that there is no such
thing as an ultimate proportion of vanishing quantities, inasmuch as before
vanishing the proportion is not ultimate, and after vanishing it does not exist
at all.... But the answer is easy... the ultimate ratio of vanishing quantities
is to be understood not as the ratio of quantities before they vanish or after
they have vanished, but the ratio with which they vanish. 16
The diagrams appeared to represent space, but
time kept creeping in: "Let the time be divided into equal parts.... If
the areas are very nearly proportional to the times. . . "
When he and Hooke had debated the paths of
comets and falling objects, they had dodged one crucial problem. All the earth's
substance is not concentrated at its center but spread across the volume of a
great sphere‑countless parts, all responsible for the earth's attractive
power. If the earth as a whole exerts a gravitational force, that force must
,ISAAC NEWTON
be calculated as the sum of all the forces
exerted by those parts. For an object near the earth's surface, some ‑of
that mass would be down below and some would be off to the side. In later terms
this would be a problem of integral calculus; in the I‑'rincipia he solved it geometrically, proving that a
perfect spherical shell would attract objects outside it exactly as by a force
inversely proportional to the square of the distance to the center.17
Meanwhile, he had to solve the path of a
projectile attracted to this center, not with constant force, but with a force
that varies continually because it depends on the distance. He had to create a
dynamics for velocities changing from moment to moment, both in magnitude and
in direction, in three dimensions. No philosopher had ever conceived such a
thing, much less produced it.
A handful of mathematicians and astronomers
on earth could hope to follow the argument. The A‑incipia's reputation for unreadability spread faster than
the book itself. A Cambridge student was said to have remarked, as the figure
of its author passed by, "There goes the man that writt a book that
neither he nor anybody else understands." 18 Newton himself said that he
had considered composing a 44popular" version but chose instead to narrow
his readership, to avoid disputations‑or, as he put it privately,
"to avoid being baited by little smatterers in mathematicks."19
Yet as the chain of proof proceeded, it
shifted subtly toward the practical. The propositions took on a quality of how to. Given a focus, find the
elliptical orbit. Given three points, draw three slanted straight lines to a
fourth point. Find the velocity of waves. Find the resistance of a sphere
moving through a fluid. Find orbits when neither focus is given. Q. E. D. gave way to Q. E. F and Q. E. L: that which was 132
'EVERY BODY PERSEVERES
to
be done and that
which was to be found out. Given
a parabolic trajectory, find a body's position at an assigned time.
'Mere was meat for observant astronomers.
On the way, Newton paused to obliterate the
Cartesian cosmology, with its celestial vortices. Descartes, with his own I‑Irincipia Philosophi&‑, was
his chief forebear; Descartes had given him the essential principle of inertia;
it was Descartes, more than any other, whom he now wished to bury. Newton
banished the vortices by taking them seriously: he did the mathematics. He
created methods to compute the rotation of bodies in a fluid medium; he
calculated relentlessly and imaginatively, until he demonstrated that such
vortices could not persist. 'Me motion would be lost; the rotation would cease.
The observed orbits of Mars and Venus could not be reconciled with the motion
of the earth. "The hypothesis of vortices ... serves less to clarify the
celestial motions than to obscure them," he concluded.20 It was enough to
say that the moon and planets and comets glide in free space, obeying the laws
of motion, under the influence of gravity.
Book III gave The System of the World. It gathered together the phenomena of the
cosmos. It did this flaunting an exactitude unlike anything in the history of
philosophy. Phenomenon 1: the four known satellites of Jupiter. Newton had
four sets of observations to combine. He produced some numbers: their orbital
periods in days, hours, minutes, and seconds, and their greatest distance from
the planet, to the nearest thousandth of Jupiter's radius. He did the same for
the five planets, Mercury, Venus, Mars, Jupiter, and Saturn. And for the moon.
ISAAC NEWTON
From the
propositions established in Book I. he now proved that all these satellites are
pulled away from, straight lines and into orbits by a force toward a center‑‑‑‑of
Jupiter, the sun, or the ear&i‑and that this forc‑e varies
inversely as the square of the distance. He used the word gravitate. "ne
. . . . . . . . . .
. . . . .
M0011 gravitates
toward the ewth and by the fcwoe of gravity, is alwavs drawn back from
rectilinear motion and kept in its
‑ ‑ ‑
‑ ‑ ‑ ‑ ‑ ‑ ‑
orbit.1121 He
performed an apple‑moon computation W‑1th. data he had lacked in
Woolsthorpe twenty years before. The moon's orbit takes 27 days, 7 hours, 43
minutes. The earth measures 123,249,600 Paris feet around. If the same force
that keeps the moon in orbit draws a falling body "in our regions,"
then a body should fall, in one second, 15 feet, 1 inch, and 17/9 lines
(twelfths of an inch). "And Iticavy bodiesdo actually descend to the
earth with this very force." No one could time a falling body with such
precision, but Newton had some numbers from beating pendulums, and, performing
the arithmetic, he slyly exaggerated the accuraCy.22 He said he had tested
gold, silver, lead, glass, sand, salt, wood, water, and wheat‑suspending
them in a pair o& identical wooden boxes ftom eleven‑foot cords and
unlinglur these pendulums so precisely that he could detect a difference of
one part in a thousand.23
.............
Furthermore, he
proposed, the heavenly bodies must perturb one another: Jupiter influencing
Saturn's motion, the sun influencing the earth, and the sun and moon both perturbing
the sea. "All the planets are heavy toward one another."24 He
pronounced:
It is now
established that this force is gravity, and therefore we shall call it gravity
from now on.
EVERY BODY
PERSEVERES
One flash of inspiration
had not brought Newton here. The path to universal gravitation had led through
a sequence of claims, each stranger than the last. A force draws bodies toward
the center of the earth. This force extends all the way to the moon, pulling
the moon exactly as it pulls an' apple. An identical force‑but toward the
center of the sun‑l'a
Keeps the earth in
orbit. Planets each have their own gravity; Jupiter is to its satellites as the
sun is to the planets. And they all attract one another, in proportion to their
mass. As the earth pulls the moon, the moon pulls back, adding its gravity to
the sun's, sweeping the oceans around the globe in a daily flood. The force
points toward the centers of bodies, not because of anything special in the
centers , but as a mathematical consequence of this final claim: that every
particle of matter in the universe attracts every other particle. From this
generalization all the rest followed. Gravity is universal.
Newton worked out
measurements for weights on the different planets. He calculated the densities
of the planets, suggesting that the earth was four times denser than either
Jupiter or the sun. He proposed that the planets had been set at different
distances so that they might enjoy more or less of the sun's heat; if the earth
were as distant as Saturn, he said, our water would freeze.25
He calculated the
shape of the earth‑not an exact sphere, but oblate, bulging at the
equator because of its rotation. He calculated that a given mass would weigh
differently at different altitudes; indeed, "our fellow countryman
Halley, sailing in about the year 1677 to the island of St. Helena, found that
his pendulum clock went more slowly there than in London, but he did not record
the difference.1126
ISAAC NEWTON
He explained the slow precession of the
earth's rotation axis, the third and most mysterious of its known motions. Like
a top slightly off balance, the earth changes the orien‑ ii tation of its
axis against the background of the stars, by about one degree every seventy‑two
years. No one had even guessed at a reason before. Newton computed the pprecesSion
as the complex result of the gravitational pull of the sun and moon on the
earth's equatorial bulge.
Into this tapestry he wove a theory of
comets. If gravity was truly universal, it must apply to these seemingly random
visitors as well. They behaved as distant, eccemtric satellites of the sun,
orbiting in elongated ellipses, crossing the plane of the planets, or even
ellipses extended to infin‑ ~fl'_‑, ity‑parabolas and
hyperbolas, in which case the cornet never would return.
These elements meshed and turned together
like the parts of a machine, the work of a perfect mechanic, like .............
an intricate clock, a metaphor that occurred to many as news of the Principia
spread. Yet Newton himself never succumbed to this fantasy of pure order and
perfect determinism. Continuing to calculate where calculation was "N
impossible, he saw ahead to the chaos that could emerge in the interactions of
many bodies, rather than just two or three. The center of the planetary system,
he saw, is not exactly the sun, but rather the oscillating common center of
gravity. Planetary orbits were not exact ellipses after all, and certainly not
the same ellipse repeated. "Each time a planet revolves it traces a fresh
orbit, as happens also with the motion of the Moon, and each orbit is dependent
upon the combined motions of all the planets, not to mention their actions upon
each other," he wrote. "Unless I am much
The
comet of 1680‑
"as observed by Flamsteed" and "corrected by Dr. Halley."
Newton also collated sightings by Ponthio in Rome, Gallet in Avignon, Ango at
La Fleche, "a young man" at Cambridge, and Mr. Arthur Storer near
Hunting Creek, in Maryland, in the confines of Virginia. "Thinking it would not be improper, I have given . . .
a true representation of the orbit
which this comet described, and of the
tail which it emitted in several places." He concludes that the tails of
comets always rise away from the sun and
"must be derived from some reflecting matter"~‑smoke, or
vapor.
mistaken, it would exceed the force of human
wit to consider so many causes of motion at the same time, and to define the
motions by exact laws which would allow of an easy calculation.1127
Yet he solved another messy, bewildering
phenomenon, the tides. He had assembled data, crude and scattered though they
were. Samuel Sturmy had recorded observations from the mouth of the River
Avon, three miles below Bristol. Samuel Colepress had measured the ebb and flow
in Plymouth Harbor. Newton considered the Pacific Ocean and the Ethiopic Sea,
bays in Normandy and at Pegu in the East Indies.28 Halley himself had analyzed
observations by sailors in Batsha Harbor in the port of Tunking in China. None
of these lent themselves to a rigorous chain of calcu‑
,ISAAC NEWTON
lation, but the pattern of two high tides per
twenty‑five hours was clear and global. Newton marshaled the data and
made his theoretical claim. The moon and sun both pull the seas; their combined
gravity creates the tides by 'A raising a symmetrical pair of bulges on
oDpositt. ‑,ide,‑, of the,
earth. Kepler had suggested a lunar influence on the seas. Galileo had mocked
him for it:
...........
That concept is completely repugnant to my mind....
I cannot bring myself to give credence to such causes as
. . . . . . . . . .
lights, warm temperatures, predominances of
occult qualities, and similar idle imaginings....
I am more astonished at Kepler than at any
other.... Tbough he has at his fingertips the motions attributed to the Earth,
he has nevertheless lent his ear and his assent to the moon's dominion over the
waters, to occult properties, and to such puerilities.29
Now Newton, too, resorted to invisible action
at a distance. Such arcana had to offend the new philosophers.
"'M
Before confronting the phenomena, Newton stated
"Rules of Philosophizing"‑rules for science, even more,,,,,,,,,‑fundamental
in their way than the laws of motion.
No
more causes qf natural things should be admitted than are,
both
true and sufficient to explain their phenomena. Do
notmultiply explanations when one will suffice. The causes assigned to natural effects of the same kind must be, so far
as possible, the same. Assume that humans and animals breathe for the same
reason; that stones fall in Amer‑
EVERY BODY
PERSEVERES
ica as they do in Europe; that light is
reflected the same way by the earth and the planets.30
But the mechanical philosophy already had
rules, and Newton was flouting one of them in spectacular fashion. Physical
causes were supposed to be direct: matter striking or pressing on matter, not
emitting invisible forces to act from afar. Action at a distance, across the
void, smacked of magic. Occult explanations were supposed to be forbidden. In
eliminating Descartes's vortices he had pulled away a much‑needed crutch.
He had nothing mechanical to offer instead . Indeed, Huygens, when he first
heard about New
ton's system of the world, replied, "I
don't care that he's not a Cartesian as long as he doesn't serve us up
conjectures such as attractions.1131 As a strategy for forestalling the
inevitable criticism, Newton danced a two‑step, confessional and
defiant.
I have explained the phenomena of the heavens
and of our sea by the force of gravity, but I have not yet assigned a cause to
gravity... I have not as yet been able to deduce ... the reasons for these
properties of gravity, and I do not feign hypotheses. For whatever is not
deduced from the phenomena must be called a hypothesis; and hypotheses,
whether metaphysical or physical, or based on occult qualities, or mechanical,
have no place in experimental philosophy... 32
So gravity was not mechanical, not occult,
not a hypothesis. He had proved it by mathematics. "It is enough," he
said, "that gravity really exists and acts according to the laws that we
have set forth and is sufficient to explain all the motions
SAAC NEWTON
................. I'll
of the heavenly
bodies and of our sea.1133 It could not he,
denied, even if its essence could not be understood.
He had declared at
the outset that his mission was to discover the forces of nature. 'He
rlediiced forces from celestial bodies'motion, as observed and recorded. He
rnadie a great claim‑the System of the World‑and yet declared his
pro‑ ........... gram incomplete. In fact, incompleteness was its
greatest virtue. He bequeathed to science, that institution in its throes of
birth, a research program, practical and open‑ _‑‑i‑i
ended. There was work to do, predictions to be computed and then verified.
"If only we
could derive the other phenomena of nature frorn
rnech;inical principles bv file same kind of reasoning. he wrote. "For
many things lead me to have a suspicion that all phenomena may depend on
certain forces by which the particles of bodies, by causes not yet known,
either impelled toward one another and cohere in regular figures, or are
repelled from one another and recede.1134 Unknown
forces‑as mysterious still as the forces he sought through his
decades‑long investigation of alchemy. His suspicion foresaw the program
of modern physics: certain forces,
attraction and
repulsion, final causes not yet known. ............
'Is He Like Other
Men?
AS THE CENTURY
BEGAN Bacon had said, "The me
chanic, mathematician, physician,
alchemist, and ma
gician all immerse
themselves in Nature, with a view to
works, but all so
far with feeble effort and slight success."'
He sought to prepare the stage
for a new type, so far
unnamed, who would
interpret and penetrate nature and
teach us how to
command it. The prototype for scientist was
not quite ready.
Halley heralded the
11yincipia in 1687 with the announcement
that its author had "at length been prevailed upon to appear in Publick.112
Indeed, Newton, in his fortyfifth year, became a public man. Willy‑nilly
he began to develop into the eighteenth‑century icon of later legend.
Halley also wrote an introductory ode ("on This Splendid Ornament of Our
Time and Our Nation, the MathematicoPhysical Treatise"). He sent a copy
to the King‑"If ever Book was so worthy of a Prince, this, wherein
so many and so great discoveries concerning the constitution of the Visible
World are made out, and put past dispute, must needs be grateful to your
Majesty'13‑and for easier reading included a summary of the explanation
of tides; James II had
ISAAC NEWTON
been Lord High Admiral before succeeding his
brother on the throne.
"The sole Principle," Halley
explained, "is no other than that of Gravity, whereby in the Earth all
Bodies have a tendency toward its Center." The sun, moon, and planets all
have such gravitation. The force decreases as the square of the distance
increases. So a ton weight, if raised to a height of 4,000 miles, would weigh only
a quarter‑ton. The acceleration of falling bodies decreases in the same
way. At great distances, both weight and fall become very small, but not zero.
The sun's gravity is prodigious, even at the immense distance of Saturn. Thus
the author with great sagacity discovers the hitherto unknown laws of the
motion of comets
............ and of the ebbing and flowing of
the sea.
Truth being uniform, and always the same, it
is admirable
to observe how easily we are enabled to make
out very
abstruse and difficult matters, when once
true and genuine
Principles are obtained.4
Halley need not have bothered. James had
other concerns. In his short, doomed reign, he was doing all he could to turn
England toward Roman Catholicism, working his will on the army, the courts, the
borough corporations and county governments, the Privy Council, and‑not
least‑the umiversities. In Cambridge he made an antagonist of Newton.
The King asserted his authority over this
bastion of Protestantism by issuing royal mandates, placing Catholics as
fellows and college officers. Tensions rose‑the abhorrence of popery was
written into Cambridge's statutes as well as its culture. The inevitable
collision came in Febru‑
IS HE LIKE OTHER MEN?
ary 1687, when James ordered the university
to install a Benedictine monk as a Master of Arts, with an exemption from the
required examinations and oaths to the Anglican Church. University officials
stalled and simmered. The professor of mathematics entered the fray‑the
resolute Puritan, theological obsessive, enemy of idolatry and licentiousness.
He studied the texts: Queen Elizabeth's charter for the university, the Act of
Incorporation, the statutes, the letters patent. He urged Cambridge to uphold
the law and defy the King: "Those that Councell'd his Majesty to disoblige
the University cannot be his true friends.... Be courragious therefore &
steady to the Laws .... If one P [apist] be a Master you may have a hundred
.... An honest Courage in these matters will secure all, having Law on our
sides.115 Before the confrontation ended, Cambridge I s vice‑chancellor
had been convicted of disobedience and stripped of his office, but the
Benedictine did not get his degree.
Newton chose a path both risky and shrewd.
Cambridge's crisis was the nation's crisis in microcosm. In England's troubled
soul Protestantism represented law and freedom; popery meant despotism and
slavery. James's determination to Catholicize the realm led to the downfall of
the House of Stuart. Within two years a Dutch fleet had invaded a divided
England, James had fled to France, and a new Parliament had convened at
Westminster‑among its members, Isaac Newton, elected by the university
senate to represent Cambridge. As the Parliament proclaimed William and Mary
the new monarchs in 1689, it also proclaimed the monarchy limited and bound by
the law of the land. It abolished the standing army in peacetime and
established a Declaration of
ISAAC NEWTON
Rights. It extended religious toleration‑‑except,
explicitly, to Roman Catholics and to those special heretics who denied the
doctrine of the Blessed Trinity. For all this Newton was present but silent.
He reported back to Cambridge an argument with numbered propositions:
1. Fidelity & Allegiance sworn to the
King, is only such a Fidelity & Obedience as is due to him by the law of
the Land. For were that Faith and Allegiance more then what the law requires,
we should swear ourselves slaves & the King absolute: whereas by the Law we
are Free men .... 6
..........................
At the nation's hub of political power, he
rented a room near the House of Commons. He put on his academic gown, combed
his white hair down around his shoulders, and had his likeness painted by the
most fashionable portraitist in London.7 Word of the 11'rincipia was spreading in the coffee‑houses and abroad. He
attended Royal Society meetings and social evenings. He met, and found a kind
of amity with, Christiaan Huygens, now in London, and Samuel Pepys, the Royal
Society's president, as well as a young Swiss mathematician and mystic, Nicolas
Fatio de Duillier, and John Locke, the philosopher in most perfect harmony with
the political revolution under way. Huygens still had reservations about the F'rincipia's resort to mysterious
attraction, but none about its mathematical rigor, and he promoted it
generously. Huygens's friend Fatio converted with loud enthusiasm to
Newtonianism from Cartesianism. Fatio began serving as an information conduit
between Newton and Huygens and took on the task of compiling errata for a revised
edition of the Principia. New‑
IS HE LIKE OTHER MEN?
ton felt real affection for this brash and
hero‑worshiping young man, who lodged with him increasingly in London and
visited him in Cambridge.
Locke had just completed a great work of his
own, An Essay Concerning Human
Understanding, and saw the I‑Wncipia
as an exemplar of methodical knowledge. He did not pretend to follow the
mathematics. They discussed theology‑Locke amazed at the depth of
Newton's biblical knowledge‑and these paragons of rationality found
themselves kindred spirits in the dangerous area of antiTrinitarianism. Newton
began to send Locke treatises on "corruptions of Scripture,"
addressing them stealthily to a nameless "Friend." These letters ran
many thousands of words. You seemed curious, Newton wrote, about the truth of
the text of 1 John 5:7: "the testimony of the three in heaven." This
was the keystone, the reference to the
Father, the Word, and the Holy Ghost. Newton had traced the passage through
all ages: interpretation of the Latins, words inserted by St. Jerome, abuses
of the Roman church, attributions by the Africans to the Vandals, variations
in the margins. He said he placed his trust in Locke's prudence and calmness of
temper. "There cannot be a better service done to the truth then to purge
it of things spurious,"8 he said‑but he nonetheless forbade Locke to
publish this dangerous nonconformist scholarship.
In disputable places I love to take up with
what I can best understand. Tis the temper of the hot and superstitious part of
mankind in matters of religion ever to be fond of mysteries, & for that
reason to like best what they understand least.
ISAAC NEWTON
Meanwhile Pepys, who found his own mysteries
in Lon‑
1_'~ ‑ ‑ ‑ ‑ ‑ ‑
‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑
don's clubs and gaming tables, came to Newton
for advice on a matter of recreational philosophy: "the Doctrine of
determining between the true proportions of the Hazards incident to this or
that given Chance or Lot." He was throwing dice for money and needed a
mathematician's guidance. He asked:
A‑has 6 dice in a Box, with which he is
to fling a 6.
B‑has in another Box 12 Dice, with
which he is to fling 2 Sixes.
C‑has in another Box 18 Dice, with
which he is to fling 3 Sixes.
Q. whether B & C have not as easy a Taske
as A, at even luck?9
.............
Newton explained why A has the best odds and
gave Pepys the exact expectations, on a wager of C1,000, in pounds, shillings,
and pence.
All these men maneuvered via friendly royal
connections to seek a decorous and lucrative appointment for Newton
............... in the capital. He pretended
to demur‑"the confinement to the London air & a formal way of
life is what I am not fond of"10‑but these plans tempted him.
London had flourished in the quarter‑century
since the plague and the fire. 'Mousands of homes rose with walls of brick,
Christopher Wren designed a new St. Paul's Cathedral, streets were widened and
straightened. The city rivaled Paris and Amsterdam as a center of trading networks
and a world capital of finance. England's trade and
146
IS HE LIKE OTHER MEN?
manufacturing were more centralized at one
urban focus than ever before or since. News‑papers appeared from coffee‑houses
and printers in Fleet Street; some sold hundreds of copies. Merchants issued
gazettes, and astrologers made almanacs. 'Me flow of information seemed
instantaneous compared to decades past. Daniel Defoe, recalling the plague
year, wrote, "We had no such thing as printed newspapers in those days to
spread rumours and reports of things, . . . so that things did not spread
instantly over the whole nation, as they do now."" It was understood
that knowledge meant power, even knowledge of numbers and stars. The esoteric
arts of mathematics and astronomy acquired patrons greater than the Royal Society:
the Navy and the Ordnance Office. Would‑be virtuosi could follow
periodicals that sprang into being in the eighties and nineties: Weekly Memorials for the Ingenious and Miscellaneous Letters Giving an Account of
the Works of the Learned. 12
Of the F'rincipia
itself, fewer than a thousand copies had been printed. These were almost
impossible to find on the Continent, but anonymous reviews appeared in three
young journals in the spring and summer of 1688,
and the book's reputation spread.13 When the Marquis de I'H6pital wondered
why no one knew what shape let an object pass through a fluid with the least
resistance, the Scottish mathematician John Arbuthnot told him that this, too,
was answered in Newton's masterwork: "He cried out with admiration Good
god what a fund of knowledge there is in that book? ... Does he eat & drink
& sleep? Is he like other men?" 14
Its publication notwithstanding, he had never
stopped working on the I‑Irincipia.
He was preparing a second edition. He scoured Greek texts for clues to his
belief that the ancients had known about gravity and even the inverse147
ISAAC NEWTON
square law. He contemplated new experiments
and sought ' ............ _2
new data for his complex theory of the moon's
motions.
Besides correcting printer's errors, he was
drafting and
. . . . . . . . . .
redrafting whole new sections, refining his
rules for philosophy. He struggled with the inescapable hole in his understanding
of gravity's true nature. He twisted and turned: "Tis inconceivable that
inanimate brute matter should
..........
(without the mediation of something else
which is not material) operate upon & affect other matter without mutual
........ ..
contact," he wrote one correspondent.
"Gravity must be caused by an agent acting constantly according to certain
laws, but whether this agent be material or immaterial is a
question I have left to the consideration of
my readers." 15 ‑ ‑‑
‑‑‑‑‑‑ ‑‑
..........
..........
He also pretended to leave to his readers‑yet
wrestled incessantly with‑the Deity lurking in his margins. God informed
Newton's creed of absolute space and absolute time. "Can God be nowhere
when the moment of time is everywhere?" he wrote in one of many new drafts
that did not see light.16 An active, interventionist God must organ‑
.............. ize the universe and the solar
system: otherwise substance would be evenly diffiised through infinite space or
gathered together in one great mass. Surely God's hand could be seen in the
division between dark matter, like the planets, and shining matter, like the
sun. All this "I do not think explicable by mere natural causes but am
forced to ascribe 1 it to the counsel & contrivance of a voluntary
Agent." 17 He returned to his alchemical experiments, too.
‑ ‑ ‑ ‑ ‑ ‑
‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑
‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑
‑ ‑ ‑
Whether or not Newton was like other men, by
the summer
of 1693 he was eating and sleeping poorly. He
had lived fifty
, ..........
IS HE LIKE OTHER MEN?
years. He was unsettled, back and forth
between the fens of Cambridgeshire and the London glare. At Cambridge his
sinecure remained intact, but he scarcely taught or lectured now. In London he
was angling for posts that required the king's patronage‑a position at
the Royal Mint, among others‑but did not fully understand his own
desires. He was uneasy in his relations with his new friends, tenuous though
these relations were, after a life with little practice in friendship. Fatio
had tormented him by falling ill and foreshadowing his own death‑"I
got a grievous cold, which is fallen upon my lungs. My head is something out of
order .... If I am to depart this life I could wish my eldest brother ... to
succeed me in Your friendship "‑and then by abruptly ending their
relationship and returning to Switzerland.18 (Fatio survived sixty years more.)
Sexual feelings, too, troubled Newton's
nights. He had long since embraced celibacy. For this he had devised a rational
program:
The way to chastity is not to struggle
directly with incontinent thoughts but to avert the thoughts by some imployment,
or by reading, or meditating on other things....
Still, unwanted thoughts came. Ceaseless
ratiocination disordered his senses.
... the body is also put out of its due
temper & for want of sleep the fansy is invigorated about what ever it sets
it self upon & by degrees inclines toward a delirium in so much that those
Monks who fasted most arrived to a state of seeing apparitions of weomen &
their shapes .... 19
ISAAC NEWTON
............. Reclusive though he remained,
rumors of Newton's mental state began to reach places where just a few years
11'f earlier his name had meant nothing: Fire had supposedly destroyed his
papers. He was in a state of frenzy or melancholy or distemper. His friends
had locked him away.20 He had lost all capacity for philosophical thought. Only
Pepys and Locke knew the truth. They received accusatory, delusional, and then
pitiable letters. First Newton wrote Pepys:
... for I am extremely troubled at the
embroilment I am in, and have neither ate nor slept well this twelve month, nor
have my former consistency of mind. I never designed to get anything by your
interest, nor by King James favour, but am now sensible that I must withdraw
from your acquaintance, and see neither you nor the rest of my friends any
more....
Then Locke:
Sir‑
Being of opinion that you endeavoured to
embroil me with woemen & by other means I was so much affected with it as
that when one told me you were sickly and would not live I answered twere
better you were dead.... I beg your pardon also for saying or thinking that
there was a designe to sell me an office, or to embroile me. I am
your most humble & most unfortunate
Servant Is. Newton 21
IS HE LIKE OTHER MEN?
Sex and ambition‑all embroiled. Madness
and genius as well; in the reputation spreading now, these imponderable
qualities reinforced each other. Pepys bruited suggestive hints. "I was
loth at first dash to tell you," he wrote one friend. He was concerned, "lest
it should arise from that which of all mankind I should least dread from him
and most lament for,‑I mean a discomposure in head, or mind, or both.1122
Yet by fall Newton delved again into
mathematical studies. He was systematizing ancient geometrical analysis: especially
the quadrature and construction of unruly curves. He continued to think of this
work as rediscovery and restoration. After all, no one had fully plumbed the
ancients' secrets. Lost manuscripts still turned up in dusty collections.
There was such grandeur and purity in these old truths, which could burst into
life, preserved across the millennium in Arabic as if in amber. "The
Analysis of the Ancients," he wrote, "is more simple more ingenious
& more fit for a Geometer than the Algebra of the Moderns.1123 Once again
Newton's own studies, even when they were most innovative, were for himself
alone. With few exceptions his treatises remained in the purgatory of his
private papers.
At the University of Oxford enthusiastic
students (but there were few) could already hear astronomical lectures on the
system of Newton.24 Not at Cambridge, however. "We at Cambridge, poor
Wretches, were ignominiously studying the fictitious Hypotheses of the
Cartesian," one fellow recalled later.25
,ISAAC NEWTON
On the continent of Europe the Newtonian
ideas were inspiring philosophers to frantic reformulations of their own
theories. "Vortices destroyed by Newton," Huygens jotted.
"Vortices of spherical motion in their place."26 He debated
mechanisms of gravity with the German mathematician and diplomat Gottfried
Leibniz, who was rushing to publish his own version of planetary dynamics.
"I noticed you are in favor of a vacuum and of atoms," Leibniz wrote.
"I do not see the necessity which compels you to return to such extraordinary
entities.1127 Newton's unmechanical gravity appalled him. "The fundamental
principle of reasoning is, nothing is
without cause," he wrote. "Some conceive gravity to signify the
attraction of bodies toward the bulk of the Earth, or their enticement towards
it by a certain sympathy.... He is admitting that no cause underlies the truth
that a stone falls towards the Earth.1128 It look Leibniz another year to brave
an approach to Newton himself. He penned a salutation in grand style across a
sheet of paper: "iflustri viro
ISAACO NEUTONO." 29
"How great I think the debt owed you,
Leibniz began. He mentioned that he, too, had been trying to extend geometry
with a new kind of mathematical analysis, "the application of convenient
symbols which exhibit differences and sums.... And the attempt did not go
badly. But to put the last touches I am still looking for something big from
you." He confessed that he had been looking everywhere for publications
by Newton. He had come across the name in a catalogue of English books, but
that was a different Newton.
Besides mathematics Newton had returned to
the most tortuous unfinished problem in the 111rincipia:
a full theory
IS HE LIKE OTHER MEN?
of the moon's motion. This was no mere
academic exercise;
given a precise recipe for predicting the
moon's place in the
sky, sailors with handheld astrolabes should
finally be able
to calculate their longitude at sea. A lunar
theory should
follow from Newton's theory of gravity: the
ellipse of the
lunar orbit crosses the earth's own orbital
plane at a slant
angle; the sun's attraction twists the lunar
orbit, apogee and
perigee revolving over a period of roughly
nine years. But
the force of solar gravity itself varies as
the earth and moon,
in their irregular dance, approach and recede
from the sun.
With a revised edition of the 1),incipia in mind, he needed
more data, and this meant calling upon the
Astronomer
Royal. Late in the summer of 1694 he boarded
a small boat
to journey down the River Thames and visit,
for the first
time, Flamsteed in Greenwich. He pried loose
fifty lunar
observations and a promise of one hundred
more. Flam
steed was reluctant, and he demanded secrecy,
because he
considered these records his personal
property. Soon New
ton wanted more‑syzygies and
quadratures and octants,
to be delivered by Flamsteed via penny post
to a carrier
who traveled between London and Cambridge
every week.
Flamsteed insisted on signed receipts. Newton
cajoled
Flamsteed and then pressured him. Revealing
the data
would make Flamsteed famous, Newton promised‑"make
you readily acknowledged the most exact
observer that has
hitherto appeared in the world." But the
data alone would
be worthless without a theory to give them
meaning‑"if
you publish them without such a theory ...
they will only
be thrown into the heap of the observations
of former
astronomers." 30 Indeed these men needed
each other
Newton desperate for data that no one else in
England could
ISAAC NEWTON
provide; Flamsteed desperate
for any sign of gratitude or respect ("Mr Ns approbation is more to me
then the cry of all the Ignorant in the world," he wrote that winter) ‑qnd
before long, they hated each other.
I ...........
"A
Two struggles
continued in parallel: Newton grappled
11 ................... ... with
Flamsteed and with a fiendish dynamicalverturbation problem. When the
astronomer complained of headaches, Newton advised him to bind his head with a
garter.31 .. .. . .... Finally he learned that Flarnsteed had let people know
about the work in progress and rebuked him bitterly:
I was concerned to
be publickly brought upon the stage about what perhaps will never be fitted for
the publick & thereby the world put into an expectation of what perhaps
they are never like to have. I do not love to be printed upon
...... . . . . .
every occasion much less to be dunned & teezed by forreigners about
Mathematical things or thought by our own
.............. 11‑1
people to be
trifling away my time .... 32
Flamsteed spilled
his agony into the margins: "Was Mr Newton a trifier when he read
IMathematicks for a sallery at Cambridge," he railed, and then added,
"Persons thinke too well of themselves to acknowledge they are beholden to
those who have furnisht them with the feathers they vrid‑‑~
themselves in.1133 Flamsteed took some small pleasure in reporting rumors of
Newton's death: "It served me to
. . . . . . . . . .
.
assure your freinds
that you were in health they haveing heard that you were dead againe." In
return, for the rest of Flamsteed's life, he was a victim of Newton's
implacable ruthlessness.
_40
,11
But Newton's fear
of raising expectations was genuine.
IS HE LIKE OTHER
MEN?
He grappled with
distortions in the data caused by atmospheric refraction. 'Me gravitational
interaction of three disparate bodies did not lend itself to ready solution.
He did ultimately
produce a practical formula for calculating the moon's motion: a hybrid
sequence of equations and measurements that appeared first in 1702, as five
Latin pages inside David Gregory's grand Astronomia
Elementa. Gregory called it Newton's theory,
but in the end Newton had omitted any mention of gravitation and buried his
general picture under a mass of details. (He began: "The Royal
Observatory at Greenwich is to the West of the Meridian of Paris 2' 19'. Of
Uraniburgh 12' 5 1' 30". And of Gedanum 18' 48'.") Halley quickly
reprinted Newton's text as a booklet in English, saying, "I thought it
would be a good service to our Nation.... For as Dr. Gregory's Astronomy is a
large and scarce Book, it is neither everyone's Money that can purchase
it." Halley hailed the theory's exactness and hoped to encourage people to
use it, but "the Famous Mr. Isaac Newton's Theory of the Moon" was
little noted and quickly forgotten.34
Newton abandoned
his Cambridge cloister for good in 1696. His smoldering ambition for royal
preferment was fulfilled. Trinity had been his home for thirty‑five
years, but he departed quickly and left no friends behind.35 As he emphatically
told Flamsteed, he was now occupied by the King's business. He had taken charge
of the nation's coin.
114
'No Man Is a Witness
,in His Own Cause
WHEN THE SEVENTEENTH CENTURY ENDED, the published
work of Isaac Newton amounted to little more than the several hundred copies of
the 11rincipia, most in England, a
few scattered on the Continent. They were not much read, but scarcity made them
valuable. Before a second edition was ready (in 1713, a quarter‑century after first publication) a copy cost
two guineas. At least one student saved his money and made a copy by hand. I
Newton's nascent legend diffused only by word of mouth in a tiny community.
When an anonymous solution to an esoteric geometry problem made its way to
Holland, Johann Bernoulli announced that he recognized the solver "ex ungue leonem"‑the lion by
his claW.2 In Berlin, Leibniz told the Queen of Prussia that in mathematics
there was all previous history, from the beginning of the world, and then
there was Newton; and that Newton's was the better haIL3 Tsar Peter of Russia
traveled to England in 1698 eager to see several phenomena: shipbuilding, the
Greenwich Observatory, the Mint, and Isaac Newton.4
The Royal Society was becalmed, its finances
ragged, its membership dwindling. Hooke still dominated. Even living
in London, Newton mostly stayed away. Yet
numerical thinking was in vogue‑calculation of all kinds was permeating
the life of the polity‑and it conjured Newton's name above all others.
Mariners, architects, and gamblers were understood to depend on mathematical
methods. Mathematics had become a pillar raising up the glory and honor of
England, "the Academy of the Universe.115 John Arbuthnot published his Essay on the Usefulness of Mathematical
Learning‑a study which, he noted, seems to require "a particular
genius and turn of head, . . . few are so happy to be born with." 'Me
incomparable Mr. Newton had now discovered "the grand secret of the whole
Machine." And he assured his readers that the world was made of number, weight, and measure‑echoing
the Wisdom of Solomon as well as William Petty~ the author of another new
tract, PoliticalArithmetick.6 Petty proposed
the application of number to affairs of state and trade; the word ceconomick barely existed, but he and
like‑minded scholars were counting what had not been counted before:
populations, life expectancy, shipping tonnage, and the national income.
Political arithmetic promised wonders, in a technological age:
One Man with a Mill can grind as much Corn,
as twenty can pound in a Mortar; one Printer can make as many Copies, as an
Hundred Men can write by hand; one Horse can carry upon Wheels, as much as Five
upon their Backs; and in a Boat, or upon Ice, as Twenty.7
A decisive technology, and the most venerable
example of standard measure, was the coin. Petty reckoned "the whole Cash
of England" at about six million pounds, circu‑
ISAAC NEWTON
lating among perhaps six million souls, and
by intricate cal
culation he showed that this was "Mony
sufficient to drive
the Trade of the Nation."
By
the end of the century, though, England's money
faced a crisis. 'Me silver penny had been the
base unit of
value for a millennium; for half that time,
the only unit. Now
gold had joined silver in supporting a
vivarium of changing
species: groats, shillings, farthings,
crowns, guineas. That
grand new coin, the guinea, was supposed to
be worth
twenty shillings, but its value fluctuated
unpredictably, as
did the price of silver. Untold quantities of
English coin
were counterfeit. Even more were shrunken in
weight and
value: worn by decades of handling or
deliberately trimmed
at the edges by professional clippers, who
then made bul
lion of their accumulated shards. So for
thirty years, new
machines, powered by horses and men‑the
mechanisms
guarded as a state secret8‑had milled a
coinage with an
ornamented rim to foil the clippers. A
mongrel currency
was the result. No one would spend a new coin
willingly;
these were mostly hoarded or, worse, melted
down for ex‑ 4
port to France. "Let one money pass
throughout the king's
dominion, and that let no man refuse,"
King Edgar had
said, centralizing England's coinage in the
tenth century.
"Let one measure and one weight be used,
such as is ob
served in London." No more. The melting
houses and press
rooms of the Mint, just inside the western
rampart of the
Tower of London, fell nearly silent as the
1690s began.
Most coins circulating were blurry hammered
silver, de
based, mistrusted, and older than the hands
through which
they passed.
The
crown called for guidance from eminent citizens,
,NO MAN IS A WITNESS IN HIS OWN CAUSE
Locke, Wren, and Newton among them. Wren
proposed a decimal system; he was ignored. The new Chancellor of the Exchequer,
Charles Montague, set a radical program in motion: a complete recoinage‑all
old coins to be withdrawn from circulation. Montague had known Newton at
Cambridge and with this support the king named him Warden of the Mint in April
1696, just as the recoinage began. Newton supervised an urgent industrial
project, charcoal fires burning around the clock, teams of horses and men
crowding in upon one another, garrisoned soldiers standing watch. It was a
tumultuous time at the Tower and in London: the terms of the recoinage had
strangled the supply of money essential to daily commerce and'. not
incidentally, effected a transfer of national wealth from the poor to the rich.
Newton grew rich himself, as Warden and then,
from 1700 onward, Master. (From his first months he complained to the Treasury
about his remuneration,9 but as Master he received not only a salary of C500
but also a percentage of every pound coined, and these sums were far greater.)
He found a house in Jermyn Street, bought luxurious, mainly crimson
furniture,10 engaged servants, and invited his twenty‑year‑old
niece, Catherine Barton, the daughter of his half‑sister, to live with
him as housekeeper. She became renowned in London society for beauty and charm.
Jonathan Swift was an admirer and frequent visitor. Within a half‑decade
she became the lover of Newton's patron Montague, by now the Earl of Halifax. I
I
By tradition the Mint posts offered easy
income; Montague had promised Newton "'tis worth five or six hundred
pounds per An, and has not too much bus'nesse to require
ISAAC NEWTON
...........
more attendance than you may spare."12
Newton did not mind treating his professorship as a sinecure‑he drew his
Cambridge salary in absentia‑but he ran
the Mint until his. . . . . . . . . . .
death, with diligence and even ferocity. He
was, after all, the
master of melters and assayers and
metallurgists who multi‑ 4~
plied gold and silver on a scale that alchemists
could only
dream of. He wrestled with issues of unformed
monetary
theory and international currency.13 There
was nothing
............
:11 lofty about the requisite arithmetic, yet few could have persevered
through the intricacies of accounting:
The Assaymasters weights are 1, 2, 3, 6, 11,
12.... The
. . . . . . . .... weight 12 is about 16 or
20 grains more or less as he
. . . . . . . . . . . . .
pleases.... His scales turn with the 128h
part of a grain, that is with the 2560th part of the weight 12 which answers
to less then the I oth part of a penny weight.... The Melter runs from 600 or
700 to 800 lb of late 1000 lb weight of silver in a pot & melts 3 potts a
day... The pots shrink in the fire ... 4 Millers, 12 horses two Horskeepers, 3
Cutters, 2 Flatters, 8 sizers one Nealer, thre Blanchers, two Markers, two
Presses with fourteen labourers to pull them.... 14
In pursuing clippers and counterfeiters, he
called on 'R
long‑nurtured reserves of Puritan anger
and righteousness.
False coinage was a capital crime, high
treason. Jane Hous
den and Mary Pitman, for example, were
condemned (but
pardoned) after having been caught with
coining tools and
trying to escape by dropping a parcel of
counterfeit money
into the Thames.15 Newton often opposed such
pardons.
Counterfeiting was difficult to prove; he had
himself made a
NO MAN IS A WITNESS IN HIS OWN CAUSE
justice of the Peace and oversaw prosecutions
himself, all the way to the gallows. William Chaloner not only coined his own
guineas but tried to cover his tracks by accusing the Mint of making its own
false money. Newton, managing a network of agents and prison informers, ensured
that he was hanged. He ignored the convict's final plea:
,'Sorne body must have lost something to
prove the Thiefe Some person robbd to prove the highwayman ... Save me from
being murthered 0 Dear Sr do this mercifull deed 0 my offending you has brought
this upon me ... 0 God my God I shall be murderd unless you wave me 0 1 hope
God will move your heart with mercy and pitty... 16
Newton did not consider the uttering of bad
money to be a victimless crime; he took it personally. For that matter, the
crown held the Master of the Mint responsible for the weight and purity of its
coinage, subject to enormous fines. At intervals he underwent the so‑called
Trial of the Pyx, named for the official coin chest, the pyx, protected by
three independent locks and keys. A jury of the Goldsmiths' Company would test
select coins "by fire, by water by touch, or by weight or by all or by any
of them," Newton noted in a memorandum he drafted and redrafted eight
times. 17 Then, with solemn ceremony, it would present the King's Council with
the verdict. Newton prepared carefully for these trials, carrying out his own
assays. They showed that he had brought the standardization of England's coins
to new heights of exactness. For the coronation of Queen Anne, in 1702, he
manufactured medals of gold and silver, for which he billed the Treasury,
twice, precisely C2,485
ISAAC NEWTON
18s.
3/2d.18 It was three years later, by Her Majesty's
Special
‑ ‑ ‑ ‑ ‑ ‑
‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑
Grace, that he was knighted.
A portent of future trouble came from
Leibniz, by second hand: "to Mr. Newton, that man of great mind, my most
devoted greeting"‑and "another matter, not only did I rec‑
‑‑ ‑ ‑ ‑ ‑‑‑‑ ‑
ognize that the most profound Newton's Method
of Flux
ions was like my differential method, but I
said so ... and
I also informed others."19 In passing
this on, the elderly
mathematician John Wallis begged Newton to
let some of
his treasure out from the darkness. Newton
was seen now as
......... ...
the curator of a hoard of knowledge, its
extent unknown.
Wallis told Newton he owed to the public his
hypothesis of
‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ I,‑
light and color, which Wallis knew he had
suppressed for more than thirty years, and much more‑a full optical treatise.
"You say, you dare not yet publish it," Wallis argued. "And why
not yet? Or, if not now, when then? You adde, lest I create you some trouble.
What trouble now, more ~‑41 then at another time? ... Mean while, you
loose the Reputation of it, and we the Benefit."
_2
His return to the Royal Society had waited,
all these years, for Hooke's exit. Hooke died in March 1703; within months Newton was chosen president. Past presidents
had often been honorary~ political figures. Newton seized power now and
exercised it authoritatively. He quickly named his own Curator of Experiments.
As president he attended almost every meeting; he commented from the chair on the
reading of almost every paper.20 He asserted control over the selection of
council members. He shored up the society's sagging finances, in part from his
own pocket. He
imposed a rule that the royal mace be
displayed when and only when he was presiding.
With Hooke dead, he also finally took
Wallis's advice and released for publication his second great work‑in
English, rather than Latin,21 and, more important, in prose rather than
mathematics. 'Mis time he needed no editor. He had three "books"
based on his work from thirty years earlier on the nature of light and color:
the geometry of reflection and refraction; how lenses form images; and the
workings of the eye and the telescope. 'Me origin of whiteness; prisms; the
rainbow. He added much more, in the form of "Queries": queries on
heat; queries on the ether; occult qualities, action at a distance, inertia.
For good measure he included a pair of mathematical papers, the first he ever
published. He titled the book Opticks‑or,
a Treatise on the Reflexions, Refractions, Inflexions and Colours of Light. He
presented it to the Royal Society with an "Advertisement" in which he
explained why he had suppressed this work since 1675. The reason: "To avoid being engaged in Disputes.1122
Not only had Hooke died but the world had
changed. Newton's style, integrating theories with mathematical
experimentation, had become familiar to philosophers, and they accepted readily
the same propositions that had stirred skepticism and scorn in the 1670s. In the Opticks Newton described his experiments vividly and revealed far
more of his working style‑at least, a plausible working style‑than
in the 11rincipia. He leaped across
optical wonders as across stepping stones: from the trigonometry of refraction
to the use of spectacles and mirrors; from thin transparent plates to bubbles;
from the composition of the rainbow to the refiraction of crystals. Much of the
available data was raw
ISAAC NEWTON
and imprecise, but he shrank from nothing:
friction, heat, putrefaction; the emission of light when bodies burn and when
their parts vibrate. He considered the mysterious property called
"electricity"‑a vapor, or fluid, or vital force that seemed to
arise from the excitation of glass, or cloth, as in his 1675 experiment with bits of paper.
But was light to be understood as waves or
particles? He still believed, hypothetically, that light was a stream of
material particles, but he explored wavy‑seeming phenomena, too:
"Do not rays of light move sometimes like an eel?" With Hooke buried,
Newton also buried the ether as a medium that might vibrate with light waves,
as a pond carries waves when struck by a stone. Such an ether would interfere
with the planets' permanent motion, otherwise so perfectly established now.
He was committed to his corpuscular theory:
that rays of light are "very small Bodies emitted from shining SubstanceS.1123
Thus he seemed to take a wrong turn: over the next two centuries, researchers
thrived by treating light as waves, choosing smoothness over granularity in
their faridamental view of energy. 'Me mathematical treatment of colors
depended on wavelength and frequency. Until, that is, Einstein showed that
light comes in quanta after all. Yet it was Newton, more than any other
experimenter, who established the case for light waves. With an accuracy measured
in hundredths of an inch, he had studied colored rings in thin filMS.24 He
found it impossible to understand this as anything but a form of periodicity‑oscillation
or vibration. Diffraction, too, showed unmistakable signs of periodicity. He
could neither reconcile these signs with his corpuscular theory nor omit them
from his record. He could not see
,NO MAN IS A WITNESS IN HIS OWN CAUSE
how a particle could be a wave, or embody waviness.
He resorted to an odd word: fits, as in "fits of easy reflection" and
"fits of easy transmission ... .. Probably it is put into such fits at its
first emission from luminous bodies, and continues in them during all its
progress. For these Fits are of a lasting nature.1125
Opticks
stretched to cosmology and metaphysics‑the more as
Newton extended it in new printings. He could speak with authority now. He used
his pulpit to issue a manifesto. He repeated again and again these dicta: that
nature is consonant; that nature is simple; that nature is conformable to
herself.26 Complexity can be reduced to order; the laws can be found. Space is
an infinite void. Matter is composed of atoms‑hard and impenetrable.
These particles attract one another by unknown forces: "It is the Business
of experimental Philosophy to find them oUt.1127 He was charging his heirs and
followers with a mission, the perfection of natural philosophy. He left them a
task of further study, "the Investigation of difficult Tbings by the
Method of Analysis.1128 They need only follow the signs and the method.
As President of the Royal Society he employed
two new Curators of Experiments.29 Sometimes he had them demonstrate or extend
features of the 11rincipia‑‑once, for example, dropping lead
weights and inflated hogs'bladders from a church tower‑but more often he
tried to spur experiments on light, heat, and chemistry. One line of experiments
explored the electric effluvium, creating a luminous glow, for example, in a
glass tube rubbed with cloth, and testing the tube's attractive power with a
feather. Some spirit, it seemed, could penetrate glass, move small objects, and
emit light‑but what? In revising the Opticks
he drafted
ISAAC NEWTON
new "Queries": for example,
"Do not all bodies therefore
abound with a very subtle, but active,
potent, electric spirit
by which light is emitted, refracted, &
reflected, electric
attractions and fugations are performed . . .
?"30 He sup . . . . . . . .
pressed these; even so, the trail of electrical
research in the
next century seemed to lead back to the Opticks.
"I have
only begun the analysis of what remains to be dis
cover'd," he wrote, "hinting
several things about it, and
leaving the Hints to be examin'd and improvd
by the far
ther Experiments and Observations of such as
are inquisi
tive."31 Active principles‑shades
of alchemy‑remained to
be found out: the cause of gravity, of
fermentation, of life
itself. Only such active principles could
explain the persist‑ ............ 11,
ence and variety of motion, the constant
heating of the sun
and the inward parts of the earth. Only such
principles
stand between us and death. "If it were
not for these Princi
ples," he wrote,
the Earth, Planets, Comets, Sun, and all
things in them would grow cold and freeze, and become inactive Masses; and all
Putrefaction, Generation, Vegetation and Life would cease. 32
. . . . . . . . . . .
Word of the Opticks spread slowly through IE=ope, then a bit faster after a
Latin edition appeared in 1706.33 Father
Nicolas Malebranche, aging theologian and
Cartesian'. I
reviewed the Opticks with the remark, "Though Mr. TNTe,,‑,,
ton is no physicist, his book is very
interesting. "34 iV, I
R;
..........
. . . ....... .
who had never managed to dispute his
madicruatics found
‑‑‑‑‑‑‑‑‑‑‑‑‑‑new
opportunities in his metaphysics. He had spok‑en of infinite space as the
"sensorium" of God, by which h, meant to unify omnipresence and
omniscience. God, being
166 ‑
‑ ‑ ‑‑‑‑‑‑ ‑ ‑
I NO MAN IS A WITNESS IN HIS OWN CAUSE
everywhere, is immediately and perfectly
aware. But the difficult word, suggesting a bodily organ for divine sensation,
left him vulnerable to theological counterattack: "I examined it and
laughed at the idea3" Leibniz told Bernoullithese eminent admirers now
turned enemies of Newton. "As if God, from whom everything comes, should
have need of a sensorium. This man has little success with MetaphysicS."35
And again Leibniz abhorred Newton's vacuum. A world of vast emptiness‑unacceptable.
Planets attracting one another across this emptiness‑absurd. He objected
to Newton's conception of absolute space as a reference frame for analyzing
motion, and he mocked the idea of gravitation. For one body to curve round
another, with nothing pushing or impelling it‑impossible. Even supernaturaL "I say, it could not
be done without a miracle."36
By now he and Newton were in open conflict.
Leibniz, four years Newton's junior, had seen far more of the world‑a
stoop‑shouldered, tireless man of affairs, lawyer and diplomat, cosmopolitan
traveler, courtier to the House of Hanover. The two men had exchanged their
first letters‑probing and guarded‑in the late 1670s. In the realm
of mathematics, it was paradoxically difficult to stake effective claims to
knowledge without disclosure. One long letter from Newton, for Leibniz via
Oldenburg, asserted possession of a "twofold" method for solving
inverse problems of tangents "and others more difficult" and then
concealed the methods in code:
At present I have thought fit to register
them both by transposed letters ... 5accd5el0efi%lli4l3m9n6oqqr8sllt9v3x:
llab3cddl0eaglOillrm7n6O3p3q6r5sllt8vx, 3aca4egh
5i4l4m5n8oq4r3s6t4vaaddaeeeeeiijmmnnooprrsssssttUU. 37
Communicating
with Leibniz: The key to the cryptogram
He retained the key in a dated
"memorandum" to himself. Still, impenetrable though this cryptogram
was, Newton had shown Leibniz powerful methods: the binomial theo . .... . ‑
..............
rem, the use of infinite series, the drawing
of tangents, and the finding of maxima and minima.
Leibniz, in his turn, chose not to
acknowledge these when, in 1684 and 1686, he published his related mathematical
work as 5'A New‑ Method for
Maxima and and Also for Tangents, Which Stops at Neither Fractions nor
Irrational Quantities, and a Singular Type of Calculus "2,1‑
‑‑‑‑‑‑‑‑‑‑
for'Mese" in the new German journal Acta Eruditorum. He
R
__R
offered rules for computing derivatives and
integrals and an innovative notation: dx, f(k), fx. This was a Pragmatic mathematics
a mathematics without proof, an al
gorithm
...............
S for solving "the most difficult and most beautiful problems."38
With this new name, calculus, it
traveled Slowly toward England, just before word of the Principia, with its classic geometrical style concealing new tools
of analysis, made its way across the Continent.
168
NO
MAN IS A WITNESS IN HIS OWN CAUSE
Now, decades later, Newton had a purpose in
publishing his pair of mathematical papers with the Opticks, and he made his purpose plain. In particular, "On the
Quadrature of Curves" laid out for the first time his method of fluxions.
In effect, despite the utterly different notation, this was Leibniz's
differential calculus. Where Leibniz worked with successive differences, Newton
spoke of rates of flow changing through successive moments of time. Leibniz was
chunklets‑discrete bits. Newton was the continuum. A deep understanding
of the calculus ultimately came to demand a mental bridge from one to the
other, a translation and reconciliation of two seemingly incompatible symbolic
systems.
Newton declared not only that he had made his
discoveries by 1666 but also that he had described them to Leibniz. He
released the correspondence, anagrams and all.39 Soon an anonymous counterattack
appeared in Acta Eruditorum suggesting
that Newton had employed Leibniz's methods, though calling them
"fluxions" instead of "Leibnizian differences." This
anonymous reviewer was Leibniz. Newton's disciples fired back in the Philosophical Transactions, suggesting
that it was Leibniz who, having read Newton's description of his methods, then
published "the same Arithmetic under a different name and using a
different notation.1140 Between each of these thrusts and parries, years
passed. But a duel was under way. Partisans joined both sides, encouraged by
tribal loyalties more than any real knowledge of the documentary history. Scant
public record existed on either side.
The principals joined the fray openly in
1711. A furious letter from Leibniz arrived at the Royal Society, where it was
read aloud and "deliverd to the President to consider
ISAAC NEWTON
the contents
thereof.1141 The society named a mitt
e‑ 51"
to investigate old
letters and papers."42 Newton provided
mrespondence with
John Collin., to 1i
t;,
theRe. Early ct _gh
"g,
Leibniz had seen
some of it, all those years before. The
. . . . . . . . . .
I
committee produced
a document without precedent: a detailed, analytical history of mathematical
discovery. No clearer account of the calculus existed, but exposition was not
the point; the report was meant as a polemic, to rondemn Leibniz, accusing him
of a whole congeries of plagiarisms. It judged Newton's method to be not only the first‑"by many
years"‑but alw more elegam, more nmrural, more geometrical,
more useful, and more certain.43 It vindicated Newton with eloquence and
passion, and no wonder: Newton was its secret author.
The Royal Society
published it rapidly. it also Published a long assessment of the report, in the Philosophical Transactions‑a
diatribe, in fact. 'Mis, too, was secrefly composed" S_ by Newton. ~Ejaus
he anonymon‑41, re‑v iewed his ourn anony~‑
mous report, and in
doing so he spoke of candor:
It lies upon
[Leibniz], in point of Candor, to tell us ‑what he means by pretending to
have found the Method before......... he had found it.
It lies upon him,
in point of Candor, to make us understand that he pretended to thi% Antiquity
of his Invention with some other Design than to rival and supplant Mr. Newton.
When he wrote those
Tracts he was but a Learner, and this he ought in candour to acknowledge.
. . . . . . . . . .
.
NO MAN IS A WITNESS
IN HIS OWN CAUSE
He declared
righteously: "no Man is a Witness in his own Cause. A Judge would be very
unjust, and act contrary to the Laws of all Nations, who should admit any Man
to be a
~544
Witness in his own
Cause.
Newton wrote many
private drafts about Leibniz, often the same ruthless polemic again and again,
varying only by a few words. The priority dispute spilled over into the
philosophical disputes, the Europeans sharpening their accusation that his
theories resorted to miracles and occult qualities. What reasoning, what
causes, should be permitted? In defending his claim to first invention of the
calculus, Newton stated his rules for belief, proposing a framework by which
his science‑any science‑ought to be judged. Leibniz observed
different rules. In arguing against the miraculous, the German argued
theologically. By pure reason, for example, he argued from the perfection of
God and the excellence of his workmanship to the impossibility of the vacuum
and of atoms. He accused Newton‑and this stung‑of implying an
imperfect God.
Newton had tied
knowledge to experiments. Where experiments could not reach, he had left
mysteries explicitly unsolved. This was only proper, yet the Germans threw it
back in his face: "as if it were a Crime to content himself with
Certainties and let Uncertainties alone."
"T'hese two
Gentlemen differ very much in Philosophy," Newton declared under cover of
anonymity.
The one teaches
that Philosophers are to argue from
Phmnomena and Experiments to the Causes thereof, and
thence to the
Causes of those Causes, and so on till we
come to the first
Cause; the other that all the Actions of
ISAAC
NEWTON
the first Cause are Miracles, and all the
Laws imprest on Nature by the Will of God are perpetual Miracles and occult
Qualities, and therefore not to be considered in Philosophy. But must the
constant and universal Laws of Nature, if derived from the Power of God or the
Action of a Cause not yet known to us, be called Miracles and occult
QualitieS?45
Newton understood the truth full well: that
he and Leib‑
11
........... ‑11 m7 had created the calculus mdepenrientIv. I _eibnif. bad not been altogether candid
about what he had learned from Newton‑in fragments, and through proxies‑but
the essence of the invention was his. Newton had made his discoveries first,
and he had discovered more, but Leibniz had done what Newton had not: published
his work for the
.............. world to use and to judge. It
was ;e_rrecv that spawned competition
and envy. `17he plagiarism controversy drev, irs, heat from the gaps in the dissemination of knowledge. Jnq young and
suddenly fertile field like the mathematics of the seventeenth century,
discoveries had lain waiting to be found, again and again by different people
in different places.46 The Newton‑Leibniz duel continued long after the
deaths of the protagonists. It constricTed the development of" English mathematics,
as orthodoxy hardened around New~ ton's dot notation.47 The more historians
came to ‑tinderstand what happened, the uglier it looked. No one could
dispute Lenore Feigenbaum's simple pr6cis: "Grown m en, brilliant and
powerful, betrayed their friends, lied shamelessly to their enemies, uttered
hateful chauvinistic slurs, 48 and impugned each others' characters."
Newton's rage, Leibniz's bitterness‑the darkest emotions of these proro‑‑~111
scientists almost overshadowed their shared achievement, :'‑" . . .
. . . . . . . . 172
NO
MAN IS A WITNESS IN HIS OWN CAUSE
Yet the priority dispute contributed to the
transition of science from private obsessions to public enterprise. It exposed
texts that Newton had meant to keep hidden and concentrated the interest of
philosophers in these new methods: their richness, their fungibility, their
power. The competition between formalisms‑superficially so different‑brought
into focus the shared underlying core.
The obsessions of Newton's later years disappointed modernity in some way. Later Newtonians came to find them as troubling as his pursuit of alchemy and biblical prophecy, if not for quite the same reasons. Just when science began to coalesce as an English institution, Newton made himself its autocrat. He purged the Royal Society of all remnants of Hooke. He gained authority over the Observatory and wrested from Flarnsteed the astronomer's own life's work, a comprehensive catalogue of the stars. (Flamsteed, summoned to appear before Newton, "complained then of my catalogue being printed by Halley, without my knowledge, and that I was robbed of the fruits of my labors. At this he fired, and called me all the ill names, puppy &c. that he could think of.1149) D. T. Whiteside, who became the twentieth century's preeminent scholar and shepherd of Newton's mathematical work, could not but remark:
Only too few have ever possessed the
intellectual genius and surpassing capacity to stamp their image upon the
thought of their age and that of centuries to follow. Watching over the
minting of a nation's coin, catching a few counterfeiters, increasing an
already respectably sized personal fortune, being a political figure, even
dictating to one's fellow scientists: it should all seem a crass and empty ambition
once you have written a 1~incipia.
ISAAC NEWTON
...............
Still, it did not seem so to Newton.50 He had
been a man on God's mission, seeking
his secrets, interpreting his design,
He but he had never meant te. draw
philmophers, to his ‑,ide_ had not meant to lead a cult or a school.
Nevertheless he, had gathered disciples and enemies as well. Leibniz neverll',~‑",'
stopped hoping for a moral victory. Adieu,
he wrote. "Adneu the vacuum, the atoms, and the whole Philosophy of M.
Newton."51
Leibniz died in 1716, having spent his last
years at Hanover as librarian to the Duke. Newton's death was still to come.
I
'The
Marble Index of a Mind
NEWS CAME SWIFTLY from far and exotic lands.
Philosophical Transactions reported
the discovery of "Phillippine‑Islands" and
"Hottentots."' Thus inspired, in 1726 a Fleet Street printer produced
a volume of Travels into Several Remote
Nations of the World, by one Captain Lemuel Gulliver, describing wonderful
peoples: Yahoos and Brobdingnagians. At length Gulliver's travels brought him
to Glubbdubdrib, the island of sorcerers, where he heard the ancients and the
moderns compare their histories.2 Aristotle appeared, with lank hair and
meager visage, confessed his mistakes, noted that Descartes's vortices were
also soon "to be exploded," and offered up some epistemological relativism:
He predicted the same fate to ATTRACTION,
whereof the present learned are such zealous asserters. He said, "that new
systems of nature were but new fashions, which would vary in every age; and
even those, who pretend to demonstrate them from mathematical principles,
would flourish but a short period of time, and be out of vogue when that was
determined."
ISAAC NEWTON
The shade of
Aristotle might think so. Never had h‑11man cosmologies come and gone so
rapidly, the new sweeping aside the old in scarcely a lifetime. Jonathan Swift
had no reason to know that Newton's would be the one to endure.
It scarcely
mattered, Voltaire said cynically. Hardly anyone knew how to read, and of
these few, hardly any read philosophy. "The number of those who think is
exceedm‑gly small, and they are not interested in upsetting the world‑"3
Nevertheless, captivated by Newtonianism, he began to spread the word in his
own writing‑popular science and myth‑making. He told the story of
the apple. whicli he had heard from Newton's niece. "The labyrinth and
abyss of . . . . . . . . . . . infinity is another new journey undertaken hy‑
Nlewrtnn and he has given us the thread with which we can find our way
through." And ‑he defended Ne%‑rton from the many French
accusers, "learned or not," who complained of his replacing familiar impulsion with mysterious attraction. He conjured a,
............. reply
in Newton's voice:
You no more
understand the word impulsion than you do the word attraction, and if you
cannot grasp why one body tends towards the centre of another, you cannot
imagine any the more by what virtue one body can push another.... I have
discovered a new property of matter, one of the secrets of the Creator. I have
calculated and demonstrated its effects; should people quibble with me
4
over the name I
give it?
Other memorialists
of Newton in England and Europe put on record personal details, of a certain
kind. The great man.qad Clea.‑ eyesight and all his teeth but one, He
hadkept
176
THE MARBLE INDEX OF
A MIND
a head of pure
white hair. He remained gentle and modest, treasuring quiet and disliking
squabbles. He never laughedexcept once, when asked what use in life was
reading Euclid, "upon which Sir Isaac was very merry." He had died,
from a stone in his bladder, after hours of agony, sweat rolling from his
forehead, but he had never cried out or complained.5
In England, where
new popular gazettes carried curiosities to the countryside, the death of
Newton inspired a decade‑long outpouring of verse, patriotic and lyrical.
He was after all the philosopher of light. Elegists seemed to give him credit
for all the colors he had found in his prism, flaming red, tawny orange,
deepened indigo. Richard Lovatt posted a poem to the Ladies Diary in 1733:
... mighty Newton
the Foundation laid,
Of his Mysterious
Art ...
Great Britain's
sons will long his works pursue.
By curious Theorems
he the Moon cou'd trace
And her true Motion
give in every Place.6
A hero, an English
hero, and a new kind of hero, brandishing no sword but "curious
theorems." The connection between knowledge and power had been made. Not
all forms of knowledge were equal: the Gentleman's
Magazine complained about schools "where the two chief branches of
Knowledge inculcated are French and Dancing," but reported with pleasure
that a medal honoring Newton had been struck at the Tower.7 More poetry
followed; an enthusiast could bring off a paean in just two lines:
Newton's no more‑By
Silence Grief's exprest
Lo here he lies;
His World proclaim the rest.8
. . . . . . . . . .
ISAACNEWTON
Alexander Pope's couplet found more readem
Nature and Nature's laws lay hid in night;
God said, Let Newton be! And All was Light. 9
Public lectures and traveling demonstrations
went where
............. the written word lacked force.
Newton had made claims that could be tested. By computation he pronounced the
earth oblate, broader at the equator, in contrast to tal: qggshaped Cartesian
earth. In 1733 the French Academy of "M Sciences propoged to settle the
nriatter and dispatched expeditions northward to Lapland and southward
to Peru with quadrants, telescopes, and twenty‑foot wooden rods.
'Ok"hen the wwagem returned‑a decade later‑they brought measurements
supporting Newton's view. Mastery of the stars
z
and planets empowered the nation's ships as
much as the wind did. Halley showed by example what it meant to believe in
Newtonianism. He made dramatic public predictions, computing the path of a certmn
comet anti prophesy‑
........... .............. ing its return
every seventy‑six years; the forecast in itself inspired and disturbed
the English long before it proved 'Al true. In I I i Hallev antic ated a
total so a ec se by pub‑
lin lishing a broadsheet map showing where
and when the moon's shadow would cross England. 'Me Royal ‑Suciet‑.y
gathered at the appointed moment in a courtyard and on a rooftop, under a clear
sky~ where they saw the sUdden
........... untimely nightfall, the sun's
corona flaring, and owls, confused, taking to the air. They saw that by
prediCting celestial
. . . . . . . . . . . . .
prodigies an astronomer tamed them and
drained them of their terror. 10
As it evolved into a new orthodoxy~
Newtonianism be‑ 'A'‑, came
a target. It was continually being disproved, in 'Llacts‑
178
THE MARBLE INDEX OF A MIND
with titles like Remarks upon the Newtonian philosophy: wherein the fallacies of the
pretended mathematical demonstrations, by which those authors support that
philosophy are clearly laid open: and the philosophy itself fully proved to be
false and absurd both by mathematical and physical demonstration." It
inspired satires, some deliberate and some ingenuously respectful. One
Newtonian convert, the vicar of Gillingham Major, wrote a treatise called Theologix Christian&‑ Frincipia
Mathematica., calculating that the probability of counterevidence to the
Gospels diminished with time and would reach zero in the year 3144. AViennese
physician, Franz Mesmer, "discovered" animal magnetism or animal
gravity, a healing principle based (so he claimed) on Newtonian principles. He
named it after himself: Mesmerism.
But Newtonianism was not yet a word, in
English.12 In Italy, an instructive little tract appeared with the title 11 Newtonianismo per le Dame, quickly
rendered into French and then English as Sir
Isaac Newton's Philosophy Explaind for the Use of the Ladies, in six
dialogues, vivid and heroic. It employed the inverse‑square law to
calculate the power of attraction between separated lovers. And the philosopher
wielded a sword after all: "Thus Sir Isaac Newton, the avowed Enemy to
imaginary Systems, and to whom you are indebted for the true idea of
Philosophy, has at one Blow lopped off the two principal Heads of the reviving
Cartesian Hydra."13
'Mat heroic style went out of vogue soon
enough. Now Poets do not glorify Newton, but they can love him, or his legend.
"Maybe he made up the apple, / Maybe not," ventures Elizabeth
Socolow:
ISAAC NEWTON
ij, I see the way
he thirsted all his life to find the force that seemed not to be there, but
acted, and precisely. 14
For centuries
between, the poets doubted him and even dernonized him‑his calculating
spirit, his icy rationahty~ his plundering of the mysteries they owned. Thi‑n Newton was
created as much by his enemies as his friends. Keats and Wordsworth joined the
Romantic artist Benjamin Haydon at dinner on a bleak December night in 1817 'N
A ‑
in his painting‑room.15
He showed them his broad, unfin‑',
ished canvas of
Christ's Entry into Yerusalem'. in fhe crowd
of,:
......... 1,__
Christ's followers
helhqd painted the~ fqep, of Newton. Keats
NJ
ragged him for that
and proposed a sardonic toast.
ton's health, and
confusion to mathematics." Newton had,
unweaved the rainbow
with his prism. He had rc‑Onced
nature to
philosophy; had made knowledge a "dull cam~;:1111111~: . , ~A_
logue of common
things"; had tried to "conquer all mystcr‑w
Ne,m,mn
ies by rule and
line."16 Shelley complained that, to 0
'g,
Those mighty
spheres that gem infinity ‑
‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑ ‑
Were only specks of
tinsel fixed in heaven
To light the
midnights of his native town! 17
He could not
acknowledge that it was Newton for whom,
the stars had grown
to mighty spheres. Wordsworth,
had an image in
mind, cold yet majestic. He saw at Trinity ,‑ id
College a statue in
the moon's light:
Newton with his
prism and silent face,
..........
The marble index of
a mind for ever Voyaging through strange seas of Thought, alone.
180
THE MARBLE INDEX OF
A MIND
Loathing Newton
most profoundly was the myth‑maker William Blake, poet, engraver, and
visionary. Blake was born to hate Newton. He loathed him and revered him. When
he drew Newton he pictured a demigod, naked and muscular, with golden locks and
keen hands. But he also saw an enemy of imagination: the lawmaker and repressorccunknown,
abstracted, brooding, secret, the dark Power hid."19 Like Leibniz and the
Cartesians he feared Newton's vacuum; unlike them, he believed in it:
"this abominable Void, this soul‑shudd'ring Vacuum." He blamed
Newton for perfection and rigidity. He blamed him for his very success as a
truthseeker. "God forbid that Truth should be Confined to Mathematical
Demonstration."20 He blamed him for departing from the particular by abstraction
and generalization. He blamed him for the reason that trumps
ISAAC
NEWTON
imagination, and he blamed him for finding
knowledge bv Y way of doubt:
Reason says Miracle; Newton says Doubt Aye
thats the way to make all nature out
............
Doubt Doubt & dont believe without
experiment.21
A
He blamed him for the part he had played‑the
Romantics,:,", 'began to see
this ‑in the a‑rit
jzr v ng of Eden, dhe mdustai!aliza‑
tion and mechanization; factories dimming the
air with, "'G smoke. Dark Satanic mills. "The Wster‑,Vneelis of
New‑Lon
"Al Blake cried:
~ .........
Of many Wheels I view, wheel without wheel,
with cogs tyrannic
Moving by compulsion each other, not as those
in Eden, which
Wheel within Wheel, in freedom revolve in
harmony & peace.1122
Newton had given, and he had taken away. He
gave a sense of order, security, and lawfulness. The American Declaration of
Independence found Newtonianism, Nia Locke, and threw it back at the British by
citing The laws of nature in its opening sentence. He gave infinite space Yet
took away the plenitude, for with infinity came the void. He took away mystery,
and for some that meant godlnic~,b, An ~59_51 ad hoc universe had also been a
providential universe.
He was made in myth, mus N em‑ton ‑of the voem No one tried reading the vast
storehouse of paper that zurnvived_1111,~. him. The manuscripts, fragmentary
drafts, scraps of calcu‑
THE
MARBLE INDEX OF A MIND
lation and speculation, all lay through the
generations in the private storerooms of English aristocratic families. 'Me
anti‑Trinitarian heresies were rumored but still secret. A full century
passed before anyone attempted a real biography: the pious David Brewster, who
in 1831 honored the nobility of Newton's genius, emphasized his simplicity, humility,
and benevolence, and, though he had seen some of the disturbing manuscripts,
declared firmly, "'Mere is no reason to suppose that Sir Isaac Newton was
a believer in the doctrines of alchemy."23
Brewster also stayed clear of the apple,
though he had heard the story and paid a visit to the surviving tree at
Woolsthorpe. It remained for the poets to ensure the apple's place in the
Newton legend. They knew the apple's ancient pull: sin and knowledge; knowledge
and inspiration. "Man fell with apples, and with apples rose," Byron
wrote‑
for
we must deem the mode
In which Sir Isaac Newton could disclose
'Mrough the then unpaved stars the turnpike
road,
A thing to counterbalance human woes;
For ever since immortal man hath glowed
With all kinds of mechanics, and full soon
Steam‑engines will conduct him to the
Moon.24
Success bred confidence. Law triumphed.
Newton's followers and successors created a more perfect Newtonianism than his
own, striving for extremes of rational‑aeterminism. In post‑Revolutionary
France, Pierre Simon de Laplace reexpressed Newton's mechanics in a form
suitable for
ISAAC NEWTON
modern field
theories‑rates of change as gradients and potentials‑and then
reached for another kind of philosopher's stone. He imagined a supreme
intelligence, a pv~rfect
11 .......... computer, armed with
data representing the positions and forces of all things at one instant. It
need only apply Nlew‑~ ton's laws: "Such an intelligence would
embrace in tite‑, same formula the‑, motions of fhe greatest bodies
ot the iiui~; verse and those of the lightest atom; nothing would bbe,",
uncertain, and the ‑hinire., like the past, V'rouild be pre‑sent
to its eyes."
Philosophers no
longer claim him as one of their ow‑nPhilosophy absorbed him, beginning
with‑ Irnmarottel Kant, who turned thc QuInall‑ tidde against T,‑,ibn;z
Pnd his chains of reasoning, theistic proofs, circles of words. Kant SaW,
_5
.......... science
as specially successftil, knowledge that heging; with experience. He brought
space and time into epistemology; space as magnitude, empty or not; time as
another kind of infinitude; both existing outside ourselves, eternal and
subsistent. To explore how we know anything, we begin,
. . . . . . . . . .
.
with our knowledge
of these absolutes. Yet afterward, Newton became a quaint figure for
philosophers. When Edwin Arthur Burtt wrote his 1924 Metaphysical Foundations of Modern
Physical Science, he first assigned those folindwions
........... to Newton and then said, without irony: "In scientific discovery
and formulation Newton was a marvelous genmusi aS a philosopher he was
uncritical, sketchy, inconsistent cvren second‑rate." He added in
passing, "It has, no doubt, bCen worth the metaphysical barbarism of a few
centuries to possess modern science.1125
The Principia marked a fork in the road: th
zipefurdi, science and philosophy went separate ways. Newton had re‑
THE MARBLE INDEX OF
A MIND
moved from the
realm of metaphysics many questions about the nature of things‑about what
exists‑and assigned them to a new realm, physics. "This preparation
being made," he declared, "we argue more safely."26 And less
safely, too: by mathematizing science, he made it possible for its facts and
claims to be proved wrong.27 This vulnerability was its strength. By the early
nineteenth century Georges Cuvier was asking enviously, "Should not
natural history also one day have its Newton?" By the early twentieth,
social scientists, economists, and biologists, too, were longing for a Newton
of their own‑or for the unattainable mirage of Newtonian perfection.28
Then science seemed
to reject that same perfection: the absolutes and the determinism. The
relativity of Einstein appeared as a revolutionary assault on absolute space
and time. Motion distorts the flow of time and the geometry of space, he found.
Gravity is not just a force, ineffable, but also a curvature of space‑time
itself. Mass, too, had to be redefined; it became interchangeable with
energy.29 George Bernard Shaw declared to radio listeners that Newtonianism
had been a religion, and now it had "crumpled up and was succeeded by the
Einstein universe.1130 T. S. Kuhn, in asserting his famous theory of scientific
revolutions, said that Einstein had returned science to problems and beliefs cc
more like those of Newton's predecessors than of his successors."31
These, too, were myths.
We understand space
and time, force and mass, in the Newtonian mode, long before we study them or
read about them. Einstein did shake space‑time loose from pins to which
Newton had bound it, but he lived in Newton's space‑time nonetheless:
absolute in its geometrical rigor
ISAAC NEWTON
and its independence of the world we see and feel. He happily brandished the tools
Newton had forged. Einstein's is no everyday or psychological relatiVity.32
"Let no one suppose," he said in 1919, "that the mighty work of Newton can really be superseded by
this or any other theory. His great and lucid ideas will retain their unique
significance for all time as the foundation of
our whole modern conceptual structure in the sphere of natural philosophy."33 The observer whom Einstein and his
followers returned to science scarcely resembled the observer whom Newton had
removed. That medieval observer had been careless and vague; time was an
accumulation of yesterdays and tomorrows,
slow and fast, nothing to be measured or relied upon. Time and space had first
to be rescued‑made absolute, true, and mathematical: The common people conceive those quantities under no other notions butfrom
the relation they bear to sensible objects. Sensible meant crude‑wooden
measuring sticks and clocks that told only the hour. And thence arise certain prejudices for the removing of which it will
be convenient to distinguish them into absolute and relative, true and
apparent, mathematical and common. The day, as measured by successive
southings of the sun, varied in
length; philosophy needed an unqualified measure. It was not only convenient
but necessary, in creating physics, to abstract this pure sense of time and space. Even so, Newton left
openings for the relativists who followed three centuries behind. It may be, that there is no such thing as an
equable motion, whereby time may be accurately measured, he wrote. It may be that there is no body really at
rest, to which the places and motions of others may be referred 34
His insistence on a particle view of light did not lead to
THE MARBLE INDEX OF A MIND
the modern quantum theory, even if, in some sense, it proved correct. It
was Einstein who discovered the equivalence of mass and energy; still, Newton suspected their organic unity:
"Are not gross Bodies and Light convertible into one another, and may not
Bodies receive much of their Activity
from the Particles of Light which enter
their Composition?"35 He never spoke offields
of force, but field theories were born in his view of gravitational and magnetic forces distributed about a center:
"an endeavor of the whole
directed toward a center, . . . a certain efficacy diffused from the center
through each of the surrounding
places.1136 Newton also anticipated the existence of subatomic forces by rejecting alternative explanations for the
cohesion of matter: "some have
invented hooked Atoms, which is begging the Question." Let others resort
to occult qualities. "I had rather infer from their Cohesion, that their
Particles attract one another by some Force, which in immediate Contact is
exceeding strong.1137 He speculated that such a forceanother force,
independent of gravity, magnetism,
and electricity‑might prevail only at the smallest distances.
The infinities, the void, the laws must
endure‑not a fashion, not reversible. We internalize the essence of what he learned. A few general
principles give rise to all the myriad properties and actions of things. The universe's building
blocks and laws are everywhere the same.38
No one feels the burden of Newton's legacy, looming forward from the past, more than the
modern scientist. A worry nags at his descendants: that Newton may have been
too successful; that the power of his
methods gave them too much authority. His solution to celestial dynamics was so
thorough and so precise‑scientists cannot help but seek
ISAAC NEWTON
the same exactness
everywhere. "A,0ight1v nnitghtv thc_,Ught
‑ ‑‑‑‑‑‑‑‑‑can
come to one's mind here," said Hermann Bondi. "The,, tools that he
gave us stand at the root of so much that
goes on now... We may not be doing a lot more than fol 10_1WkX111‑tg::"
in his footsteps. We may still be so much under the i m‑pres Sion of the
particular turn he took ... we cannot get it 011t Of , our system.1139 We
cannot. What Newton learned e‑n‑r‑e‑red the marrow of
what we know without knowing how WiVe_ know it.
N
His papers began to
appear in the early twentieth century~: when cash‑poor nobility sold them
at aucido‑ n and thev s cat~ tered to collectors in Europe and across the
Atlantic. In 1936 Viscount Lymington, a descendant of Catherine Bav‑
‑ ‑‑‑‑‑‑
‑ ‑ ‑
ton', sent
Sorheby's a meTal Trunk containing manuscripts of three million words, to be
broken up and offered at auction in 329 lots. Interest was slight,40 but the
economist and ~~21'1_~' Cantabrigian John Maynard Keymes, disaurbed, a% he
said,,"" by the impiety~ managed to buy some at the auction and, then
gradually reassembled more than a third of the
collection. What he found there amazed him: the 2kN!M1.%t,‑ the
heretical theologian; not the cold rationalist Blake had so despised but a
genius more peculiar and extraordinary. An
..................
"intense and flaming spirit." With the papers Keynes alSID bought
Newton's death mask‑eyeless, scowling. At least twenty portraits of
Newton had been painted, not all frotn"11111 life; they differ
extravagantly, one from another.
"Newton was
not the first of the age of reason," Keynes, told a few students and
fellows in a shadowed room at Trinity College. "He was the last of the
magicians, the last of the Babylonians and Sumerians, the last great mind
which,
188
looked out on the
visible and intellectual world with the same eyes as those who began to build
our intellectual inheritance rather less than 10,000 years ago.1141 The Newton
of tradition, the "Sage and Monarch of the Age of Reason," had to
arise later.
ISAAC NEWTON
He had concealed so
much, till the very end. As hi‑s health declined, he kept writing.
His niece's newhilgbind John Conduitt, saw him in his last days working
in near
............ ‑darkness
on an obsessional history of the world‑he vvrote at least a dozen drafts‑The
Chronolog_v qf Ancient Kingdoms, Amended.
42 He measured the reigns of kings and the generations of Noah, used
astronomical calculations to date the"'‑_
qailiTilz of the Argonants, and declared the ancient kingdoms' to be
hundreds of years younger than generally supposed. He incorporated his analysis
of the Temple of Solomon and said
enough about idolatry and the deification of king$ to,,",E,‑‑,,1_
raise suspicion of his heretical beliefs. but he suppresse those one last time.
In his chambers,
after a painful fit of gout, he sat Conduitt before a wood fire and talked
about comets. sun needed constant replenishment, he said. Comets mus provide
it. feeding the sun like logs thro‑wn
on the fire. The', comet of 1680 had come close, and it would return. e, that
on one approach, perhaps after five or Six more‑ or‑~ bits, it
would fall into the sun and fuel a blaze to cons the very earth, and all its
inhabitants would perish in e,,'.`~,~;........... flames.43 Yet, Newton said,
this was mere conjecture.
He wrote: "To
explain all nature is too difficult a task fbrl_~.,~,., any one man or even for
any one age. Tis much better to do
'g, a little with
certainty & leave the rest for others that c after yoU.1144 This sheet of
paper, too, he abandoned.
On his deathbed he
refused "'he ‑r‑raent
of die drlur
" . . ..... . .... Nor could a
pair of doctors ease his pain. He ie ear Sunday morning, March 19, 1727. On
Thursday e Royat Society recorded in its Journal Book, "The Chair
beingglll~'?,'11 Vacant by the death of Sir Isaac Newton there was no Meeting
this Day."
THE MARBLE INDEX OF
A MIND
I‑Iis recent
forebears had used scriveners to draft wills directing the disposition of their
meager possessions, principally sheep. When they did not leave such documents,
even their names vanished. An early chronicler, researching Newton's story soon
after his death, delved into the Woolsthorpe parish registers of births and
burials and found almost nothing: the information "lost, destroyd, or
obliterated; for want of care and due preservation." The national
records, he railed, were "the most neglected! ... committed to a parish
clark, illiterate, that can scarcely write, sottish, or indolent: a task on
which the fortunes and emoluments of the whole kingdom in a great measure
depends." In an old town chest, a tattered vellum leaf bore this datum
under the heading baptizU anno 1642: "Isaac
sonne of Isaac and Hanna Newton Jan 1.1145
In eighty‑four
years he had amassed a fortune: household furniture, much of it upholstered in
crimson; crimson curtains, a crimson mohair bed, and crimson cushions; a
clock; a parcel of mathematical instruments and chemical glasses; several
bottles of wine and cider; thirty‑nine silver medals and copies in
plaster of Paris; a vast library with nearly two thousand books and his many
secret manuscripts; gold bars and coins‑the whole estate valued
atC31,821,46 a considerable legacy.
Yet he left no
will.